Двухплоскостная балансировка двумя парами грузов

Двухплоскостную балансировку чаще всего проводят с помощью вычислений в специализированных программах. Задача - определить чувствительности к пробным грузам в обеих балансировочных плоскостях и рассчитать корректирующие груза. Но в данной статье хочу осветить один из способов динамической двухплоскостной балансировки жесткого межопорного ротора без использования программ. Уверен, многим специалистам он покажется как минимум интересным. Как всегда на реальном практическом примере на месте эксплуатации. В качестве подопытного выступит вентилятор двухстороннего всаса на ременной передаче (n = 3000 об/мин).

Немного теории

Как известно, динамический дисбаланс является суммой статической и моментной составляющих. Суть данного способа - поочередное устранение статического и моментного дисбалансов установкой двух пар грузов. При этом, для устранения статики используется симметричная пара одинаковых по массе, радиусу и углу установки грузов разнесенных по двум плоскостям, а для устранения моментной составляющей используется кососимметричная пара - два груза, разнесенных по двум плоскостям, одинаковых по массе и радиусу установки, но расположенных под углом 180° друг к другу.

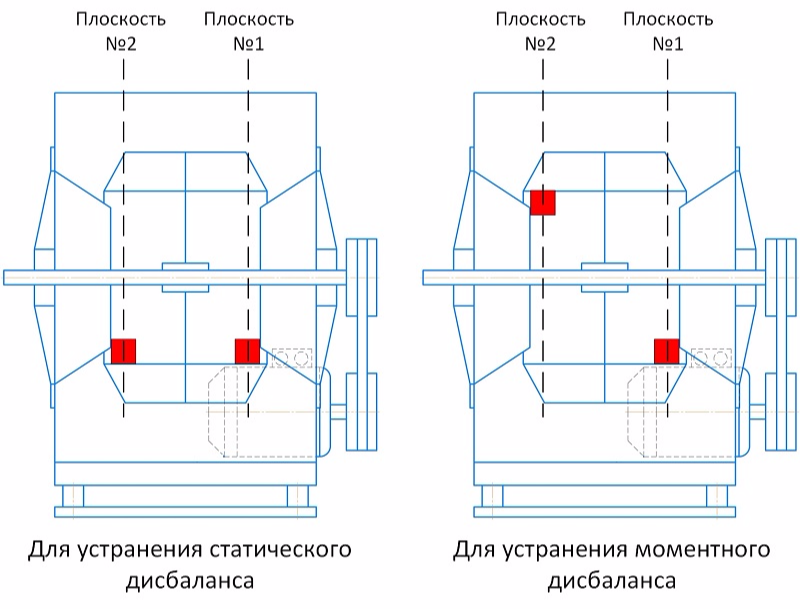
Балансировка проводится для одного направления измерений (например, только для вертикального или только горизонтального). Для разделения динамического дисбаланса на статическую и моментную составляющие нам необходимо выполнить следующие векторные построения:

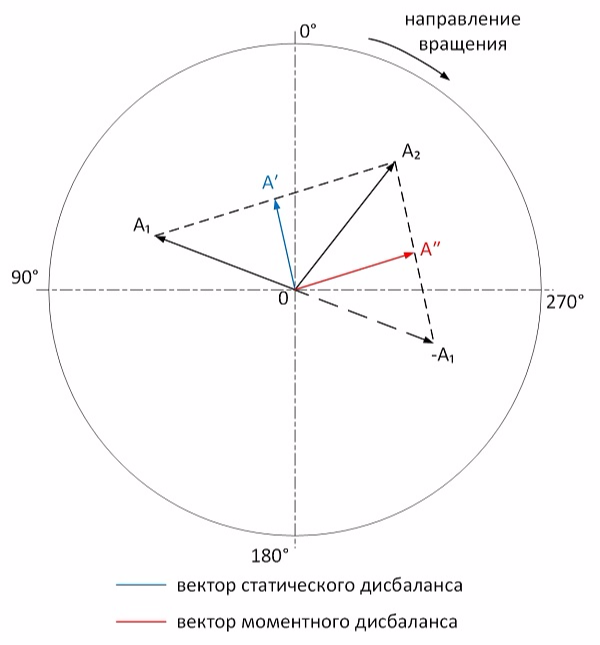
А₁ и А₂ - вектора вибрации опор №1 и №2 соответственно. Доказано, что полусумма этих векторов является статической составляющей, а их полуразность - моментной. Поэтому, вектор А′, проведенный к середине отрезка соединяющего вершины векторов А₁ и А₂ и являющийся их полусуммой - вектор статического дисбаланса. В свою очередь, вектор А″, проведенный к середине отрезка соединяющего вершины векторов -А₁ и А₂ (полуразность А₁ и А₂) - вектор моментного дисбаланса.

Далее балансировка проводится в следующем порядке. Произвольно выбирается какую из составляющих (А′ или А″) балансировать первой. Устанавливается соответствующая пробная пара грузов. Полученные вектора вибрации пробного пуска так же раскладываются на составляющие. Если, например, мы сначала хотим устранить статическую неуравновешенность используя пару симметричных грузов, то строим вектор влияния на статическую составляющую. По соотношению длин векторов начального статического дисбаланса и вектора влияния пробного груза на статику определяем массу пробных грузов, по углу между этими векторами определяем угол, на который необходимо переместить оба груза. Расчет как при обычной балансировке с той лишь разницей, что оба груза считаем как один. После устранения статики аналогично выполняется балансировка моментной неуравновешенности. Более понятно станет на практическом примере.

Практический пример

Так получилось, что завод-производитель не смог устранить вибрацию на поставленном вентиляторе в составе приточной установки. Дважды забирали оборудование на завод, дважды балансировали вентилятор, но вибрация так и осталась высокой. Не буду гадать о причинах, самое главное что появилась возможность опробовать этот способ балансировки и разбавить рутинные будни вибрационщика чем-то интересным. Здесь опущу процедуру вибродиагностики и устранения других дефектов, так как интересна только балансировка вентилятора.

Исходные данные

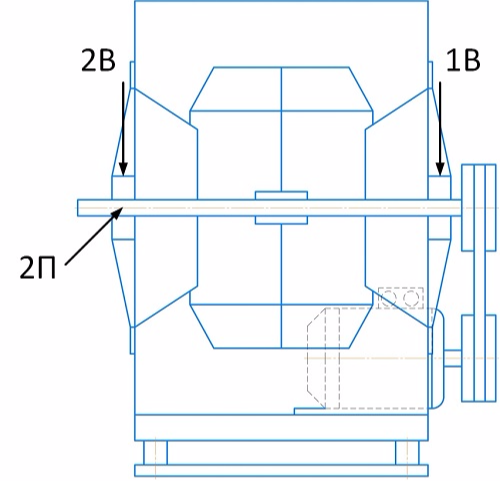
Измерения амплитуды/фазы оборотной составляющей вибрации для балансировки производились по следующим точкам:

Пуск 0. Данные измерений амплитуды/фазы оборотной частоты (виброскорость, мм/с):

Конструкция крепления опоры №1 вентилятора не позволяет выполнить измерения в поперечном направлении. В связи с этим выбор направления для балансировки очевиден - вертикальное. По точке 2П будем отслеживать изменение вибрации в поперечном направлении.

Оценим фазы вибрации в вертикальном направлении. При статическом дисбалансе разность фаз в точках 1В и 2В должна стремиться к 0°, при чистом моментном дисбалансе к 180°. Фактическая разность фаз 109°. Предварительно можно сделать вывод, что моментной неуравновешенности чуть больше чем статической. Используя балансировочный круг выполним построения для определения статической и моментной составляющих дисбаланса:

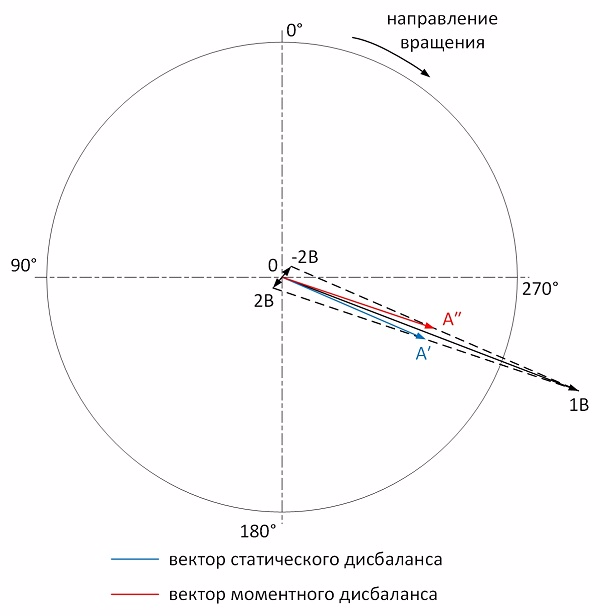
Как видим, моментной неуравновешенности и вправду чуть больше чем статической. Начнем балансировку с устранения статического дисбаланса.

Статическая балансировка

Пуск 1. В качестве пробного груза устанавливаем симметричную пару грузов массой по 4,7 грамм на угол 0°:

Графически определяем вектор влияния пробной симметричной пары грузов на статический дисбаланс. Он будет являться отрезком соединяющим вершины полусумм векторов пуска 0 и пуска 1:

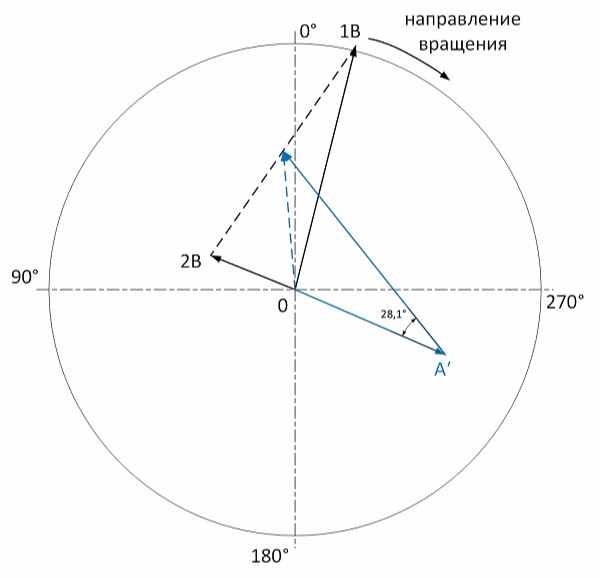
Соотношение длины вектора статического дисбаланса к длине вектора влияния равно 0,63. Соответственно каждый груз из симметричной пары необходимо уменьшить до 4,7x0,63=2,9 грамм. В соответствии с рисунком пару грузов необходимо развернуть на 28° против вращения. Поскольку расчет делал вручную, то ошибся и получил угол 33°.

Пуск 2. Установлена симметричная пара грузов массой по 2,9 грамма на угол 33°:

Производим векторные построения:

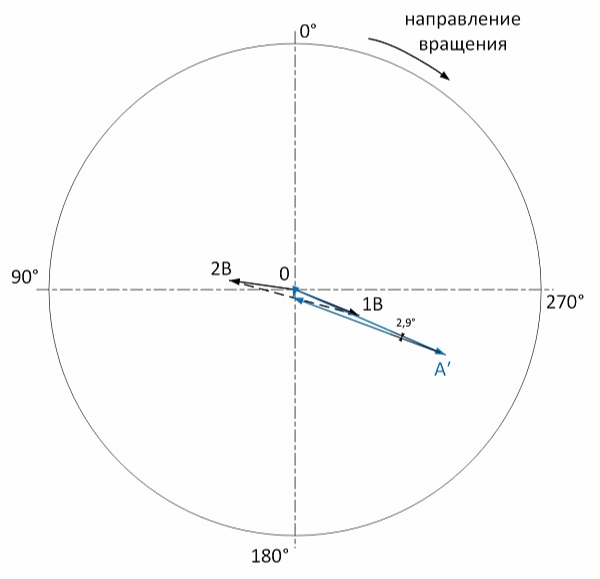
Судя по рисунку, вектором влияния практически попали в 0. Остаточный статический дисбаланс составляет 0,3 мм/с. На этом статическую балансировку считаем оконченной.

Моментная балансировка

Вибрация пуска 2 является исходной для уравновешивания моментной составляющей. Определим ее (далее увеличиваем масштаб в 2 раза):

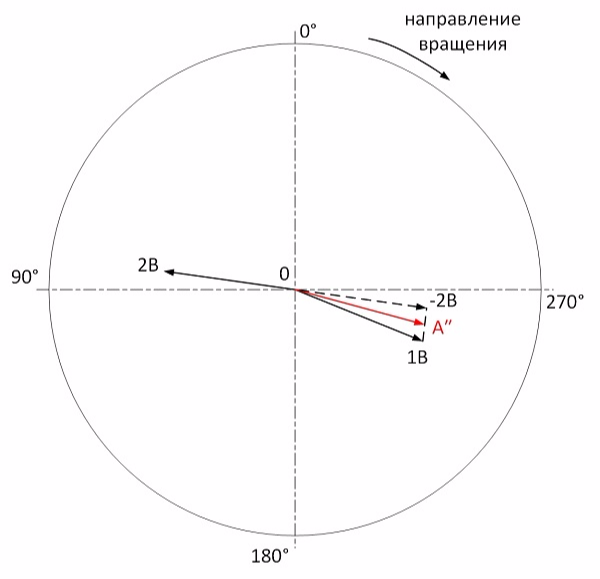
Пуск 3. В качестве пробного груза устанавливаем кососимметричную пару грузов массой по 4,8 грамма на угол 0° в плоскости №1 и 180° в плоскости №2:

Расчет проводим аналогично. Определяем вектор влияния пробной кососимметричной пары грузов:

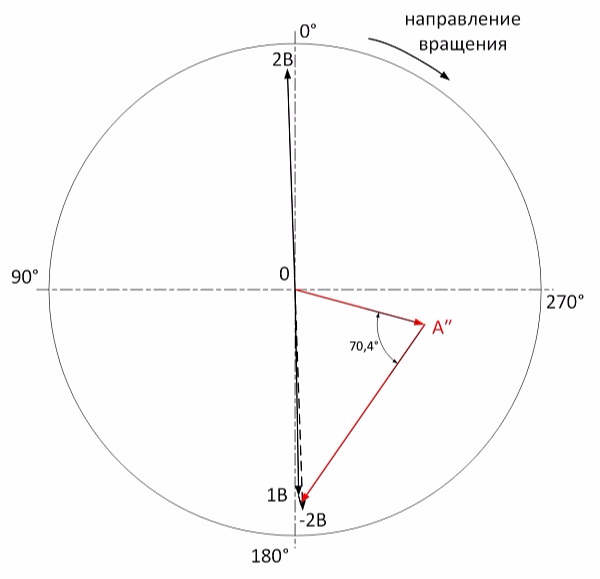
Отношение вектора моментного дисбаланса к вектору влияния равно 0,62. Из этого следует, что расчетный груз составляет 4,8x0,62=3,0 грамм. Дополнительно необходимо повернуть систему грузов на угол 70° по вращению. Ручной расчет приводит к погрешностям и по месту я получил угол 66°.

Пуск 4. Установлена кососимметричная пара грузов массой по 3,0 грамма на угол 294° в плоскости №1 и угол 114° в плоскости №2:

Выполним векторные построения:

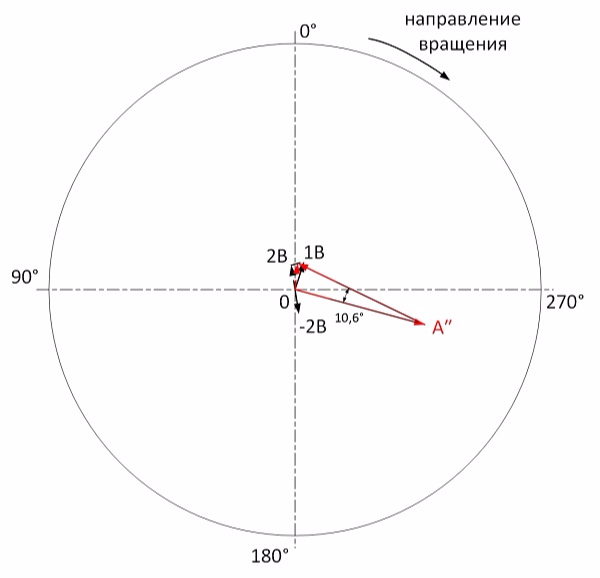
Исходя из рисунка, амплитуда моментного дисбаланса составляет порядка 0,5 мм/с. На этом балансировка окончена.

Исходный дисбаланс снижен более чем в 20 раз. Данный способ динамической балансировки двумя парами грузов показал свою точность и надежность. При отсутствии балансировочных программ этот способ является лучшим для уравновешивания жестких межопорных роторов.