Применение модального анализа на практике

Данную статью хочу посвятить практическому применению модального анализа. Никогда модальным анализом не занимался, не было приборов с соответствующими функциями, их и сейчас нет и не предвидится. Очень дорого. Но это не повод отчаиваться и ставить на таком интересном методе крест. Решением проблемы является 3D-моделирование и расчет мод колебаний. Как я к этому пришел, как это сделать и что в итоге получится - читайте далее.

Описание проблемы

Имеем 4 центробежных насоса ЦН 65/90 с электродвигателями N = 37 кВт, n = 3000 об/мин. На трех из них проблема с повышенной вибрацией электродвигателей. Вибрация высока и на холостом ходу, и в сборе с насосами.

Исходные данные

В качестве иллюстрации проблемы возьмем данные прокрутки одного из электродвигателей на холостом ходу на месте эксплуатации.

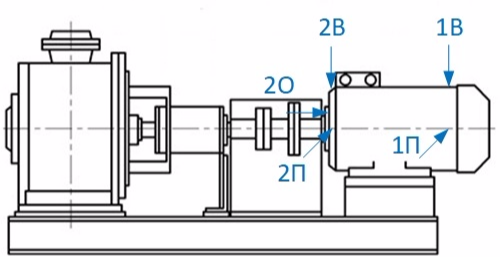
СКЗ виброскорости в диапазоне 10-1000 Гц, мм/с:

Спектры виброскорости во всех точках контроля:

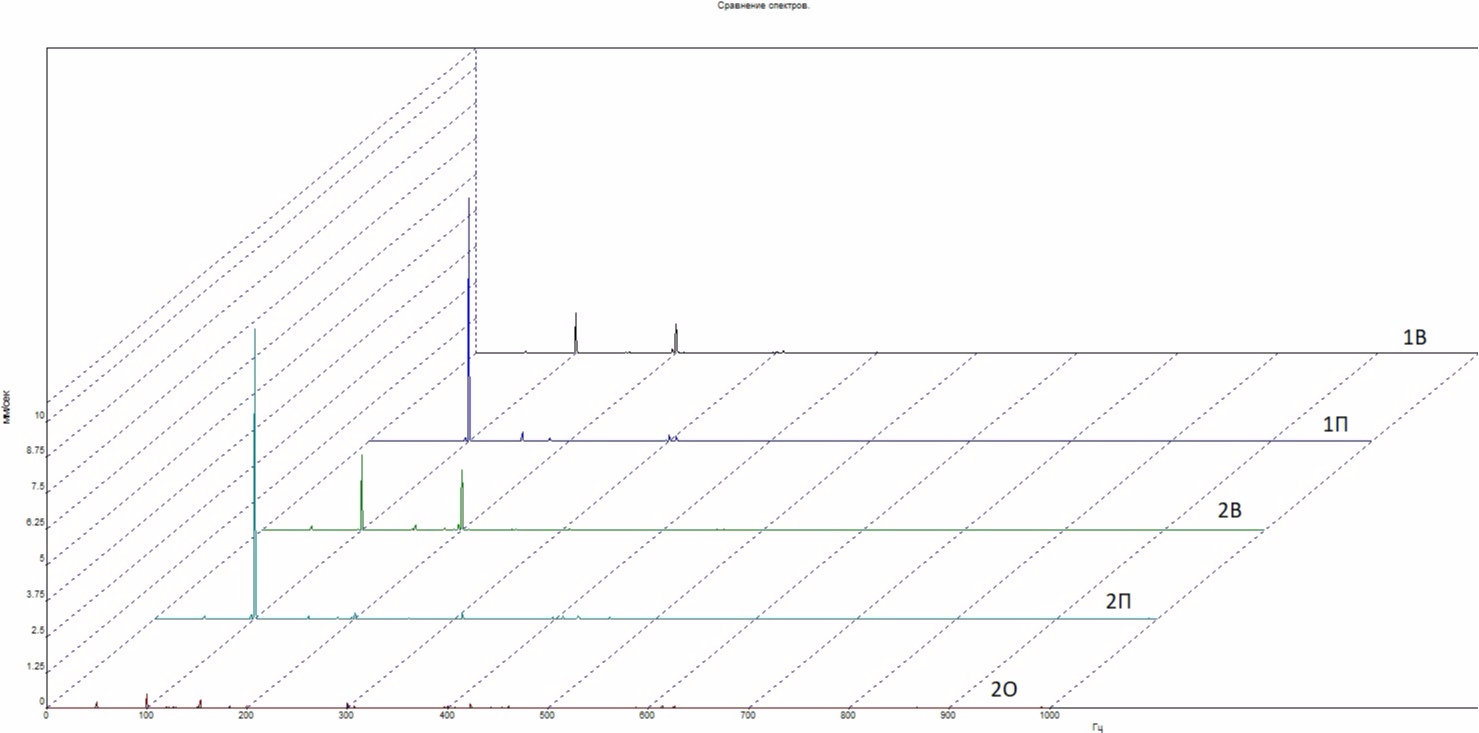
В спектрах доминирует составляющая 100,0 Гц, в вертикальном направлении также заметна 200,0 Гц. Работа электродвигателя сопровождается сильным гулом.

Анализ

Ослабляем крепления лап электродвигателя:

Гул прекратился. Ситуация очень похожа на такой дефект, как мягкая лапа. Но на аналогичных электродвигателях мягкую лапу пытались устранить - шабрили раму для выравнивания поверхностей под лапами. Проблема повышенной вибрации не была решена. Из своего опыта могу сказать, что мягкая лапа в подавляющем большинстве случаев не вызывает очень высоких уровней вибрации.

При затяжке мягкой лапы мы искривляем корпус, что изменяет зазор между ротором и статором электродвигателя и искажает электромагнитное поле, вызывая вибрацию на двойной частоте сети 100 Гц. Поэтому мы практически на всех электродвигателях в прямых спектрах видим 100 Гц в поперечном (горизонтальном) направлении. Но высокой виброактивности мы достигаем при резонансе. При ослаблении крепления лапы у нас лишь уменьшается жесткость, что изменяет собственную частоту и ослабляет/устраняет резонанс. И вот в этом моменте многие вибродиагносты путаются, считая, что если при ослаблении лапы электродвигателя вибрация падает, то этот дефект ни что иное как мягкая лапа. Не точный диагноз приводит к бесполезным трудоемким работам (шабрят раму или лапы двигателя).

Тестом на удар определяем собственные частоты в поперечном направлении (в точке 2П):

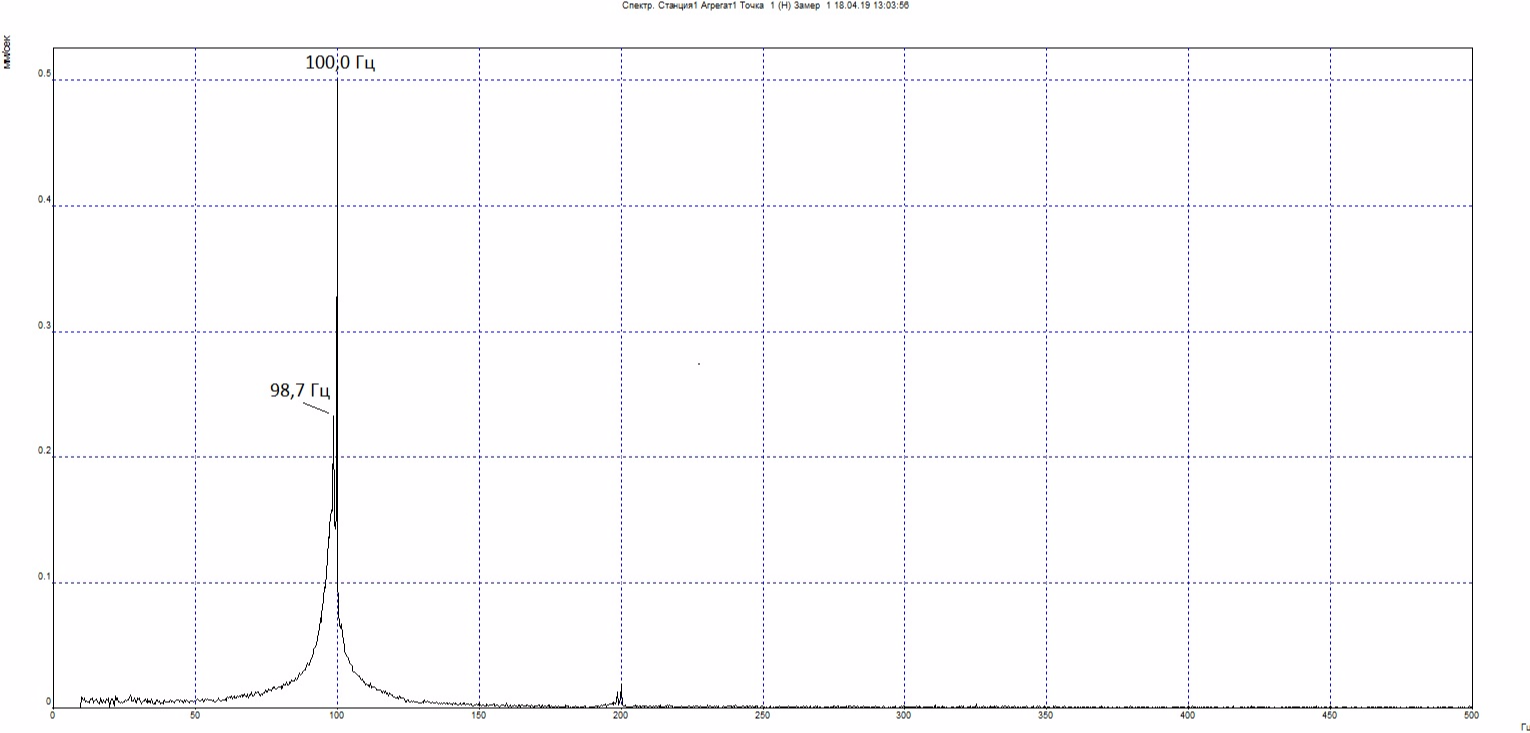
Пик 100,0 Гц очень узкий и, вероятно, является следствием наведенной вибрации. А вот широкий пик с максимумом 98,7 Гц является собственной частотой в поперечном направлении. Резонанс подтвержден.

Дополнительно определим собственную частоту в осевом направлении (в точке 2О):

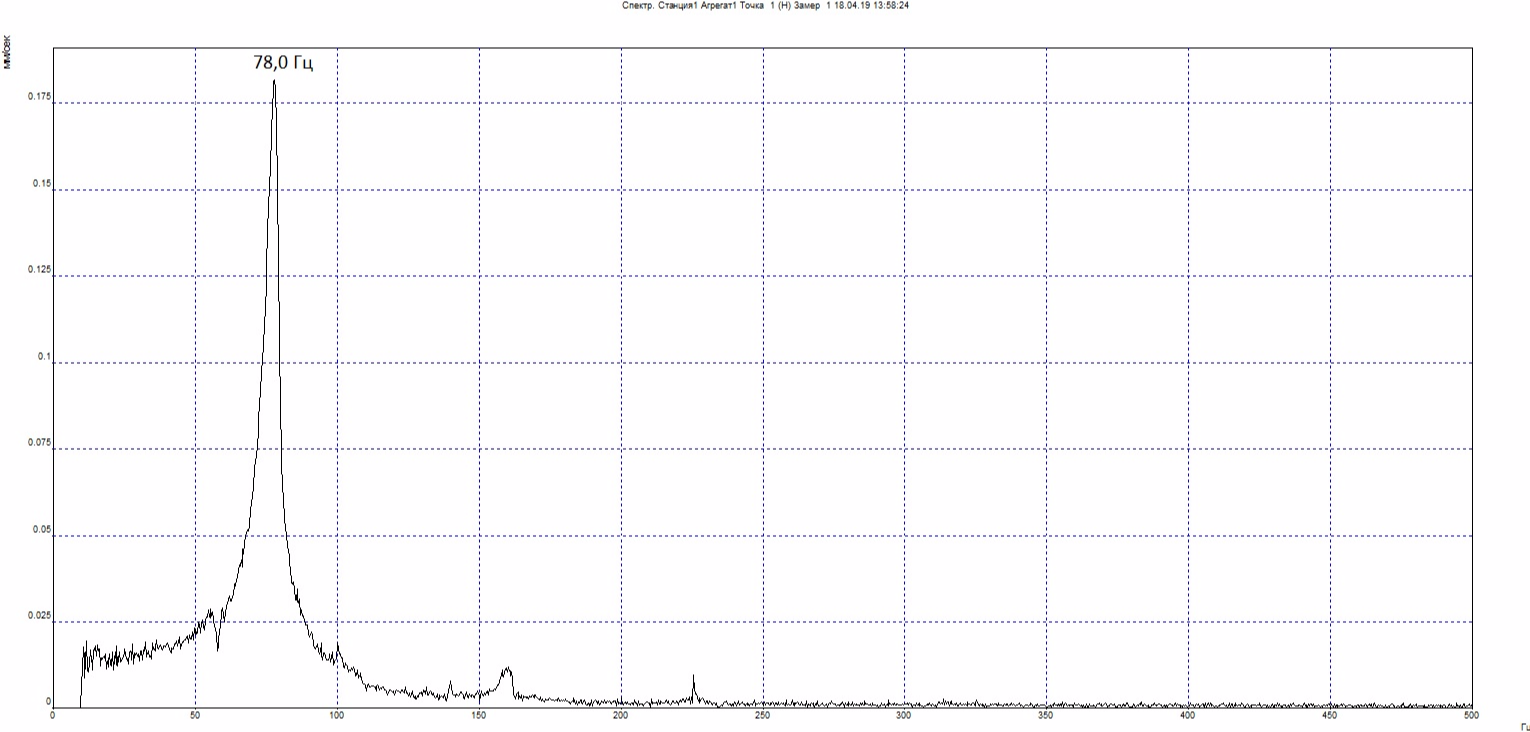
Запомним собственную частоту 78,0 Гц, она пригодится нам позже.

В вертикальном направлении тест ударом проводить не стал - оребренная поверхность и коробка борно мешают нормально выполнить эту операцию.

Итого, имеем резонанс.

Временное решение

Далее владелец оборудования дал команду сочленять муфтовое соединение и выполнить прокрутку агрегата в сборе. Результат остался тем же - повышенная вибрация в поперечном направлении. На этот раз я не согласился ослаблять крепление лап и предложил для отстройки от резонанса усилить швеллер рамы под электродвигателем самодельными домкратами (шпильки с гайками на концах). Вибрация снизилась до 3-4 мм/с, в таком состоянии все осталось и по сей день.

Модальный анализ

Как Вы понимаете, такое решение меня не устраивает. Необходимо найти коренную причину резонанса. Как я писал выше, один из четырех насосов работал без претензий к вибрации. Визуально все насосы и их фундаменты выглядят одинаково.

Так как я уверен, что проблема носит структурный характер, то для идентификации причины было бы неплохо увидеть моду колебаний на частоте 100,0 Гц. В приборах Кварц/Топаз такой функционал, естественно, отсутствует. Но ведь проектировщики как-то проводят расчет конструкций, механизмов и узлов на собственные частоты. Где-то в интернетах видел красивые картинки с расчетами форм колебаний в разных CAD-системах. Уверен, что это несколько проще, чем ракету строить, да и для самообразования не помешало бы попробовать смоделировать свою проблему.

Когда-то в институте я неплохо чертил в Компас-3D. И оказалось, что в эту замечательную программу уже завезли модуль APM FEM - приложение для выполнения экспресс-расчетов твердотельных объектов и визуализации результатов этих расчетов. Пробуем.

Сбор исходных данных

Поскольку стоит задача выполнить расчет максимально точно, то для построения 3D-модели требуются реальные размеры рамы и электродвигателя. Выполняю снятие геометрических размеров:

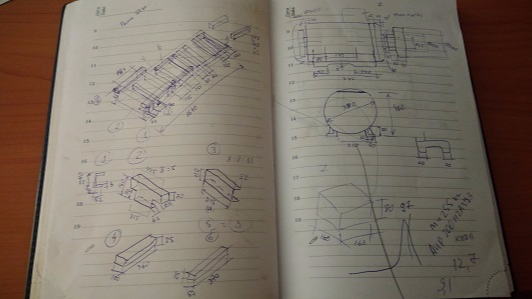
Создание 3D-модели

В Компас-3D по геометрическим размерам строю 3D-модель:

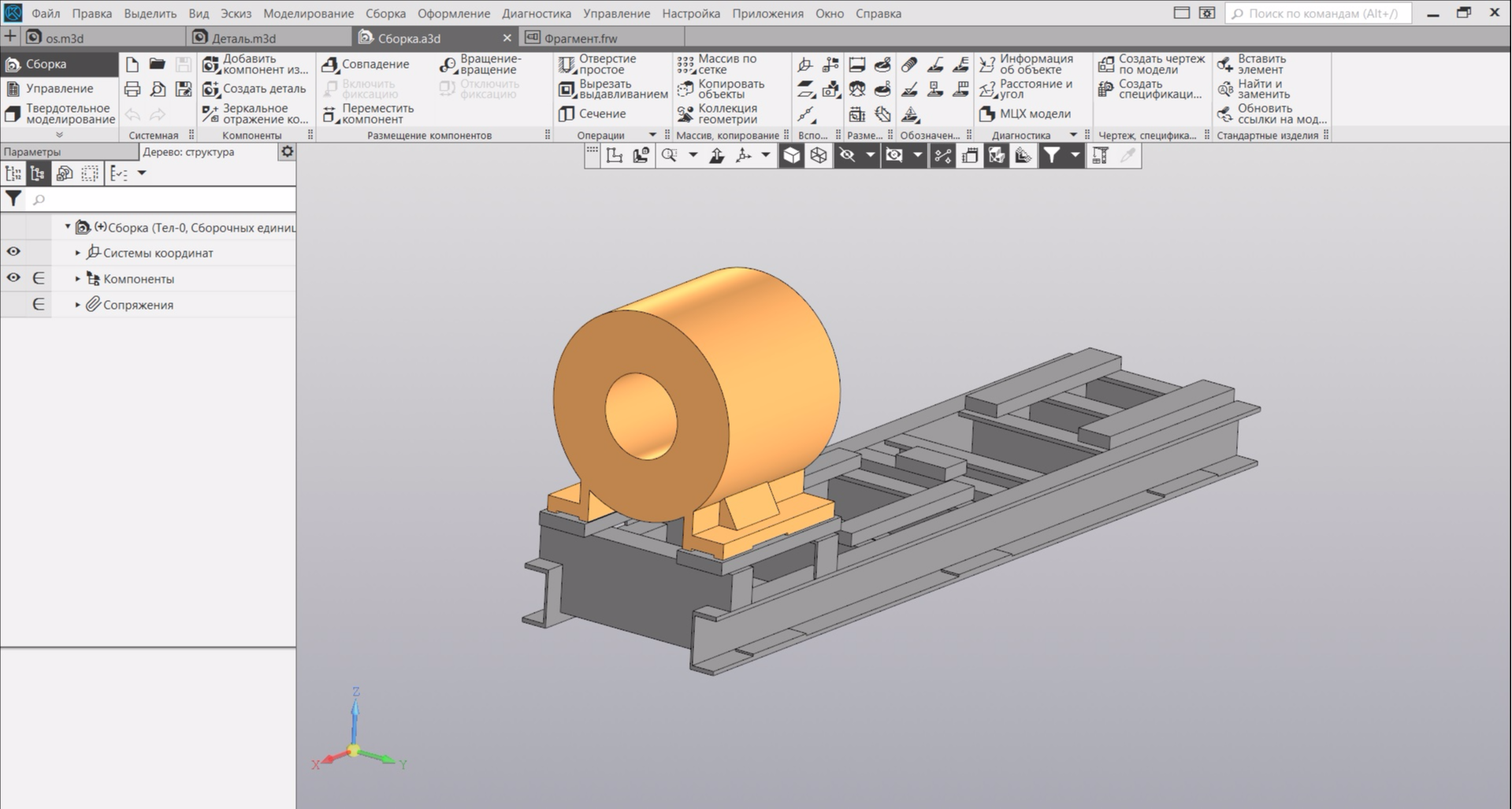
Электродвигатель полностью прорисовать - очень времязатратно. Поэтому точно прорисовываю его лапы, а сам корпус заменяю на цилиндр. При этом внутренний диаметр цилиндра подбираю таким образом, чтобы в модели масса электродвигателя равнялась паспортной. Насос находится на другом конце рамы и вряд ли влияет на собственные частоты электродвигателя, поэтому обойдемся без него.

Расчет в APM FEM

Далее в приложении APM FEM выбираем места закрепления рамы - площадки, к которым прижимаются гайки анкеров фундамента:

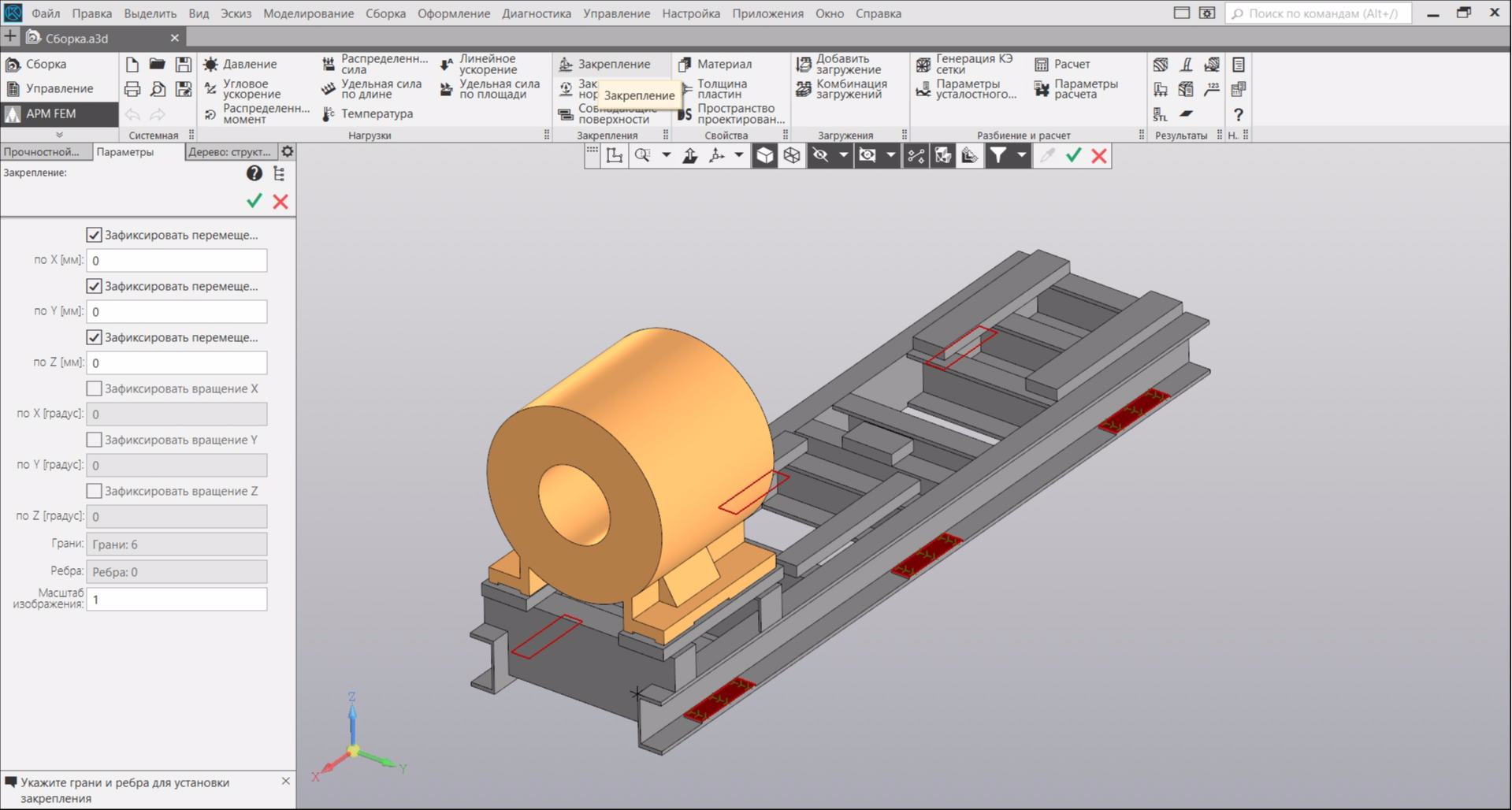
Переходим к генерации сетки конечных элементов (КЭ-сетки). Я выбрал параметры сетки, указанные на рисунке ниже. Уменьшение размеров элементов и усложнение их формы повысит точность расчета, но в дальнейшем увеличит время и потребление памяти.

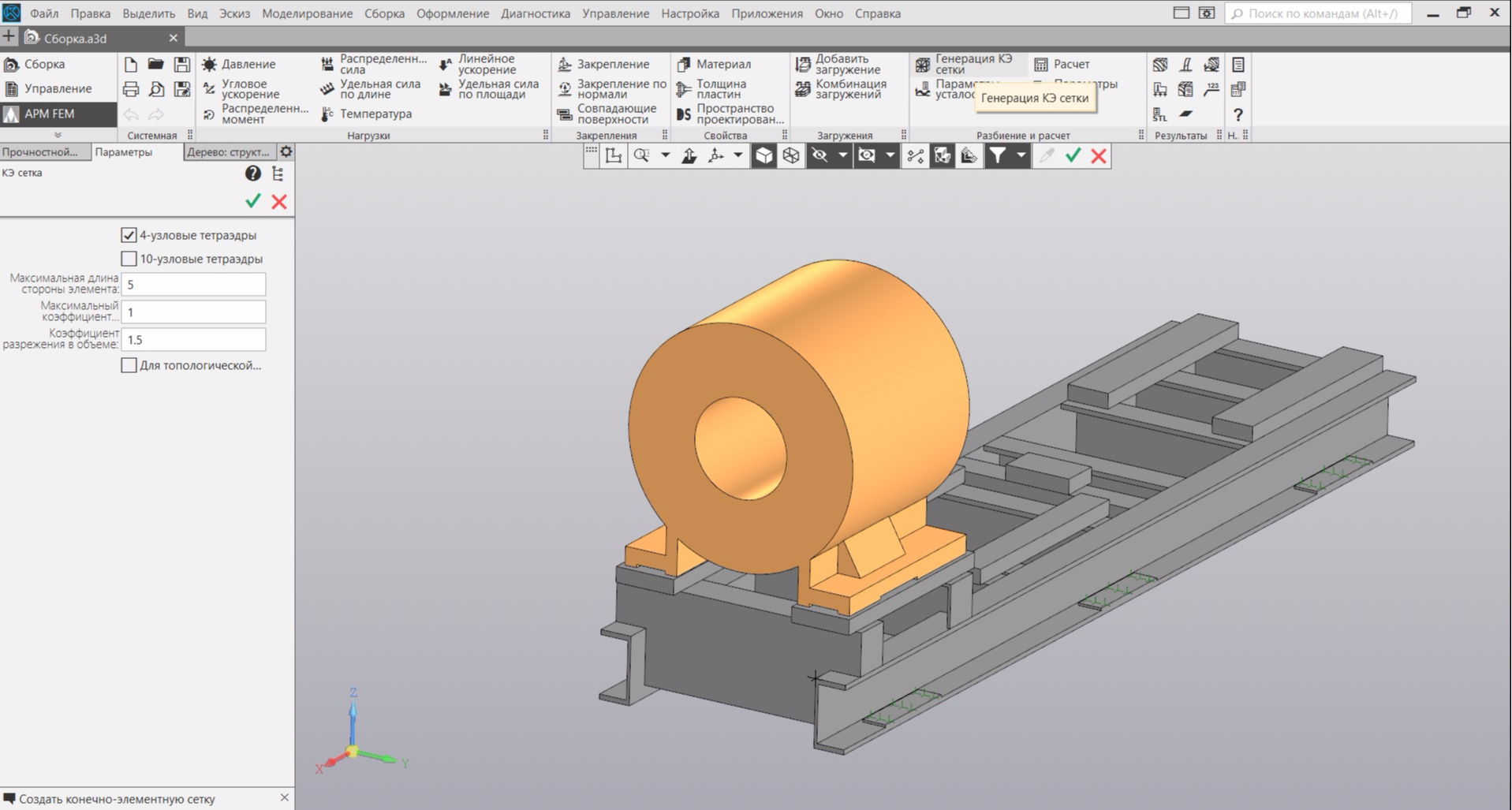
Если Вы не указывали материал элементов модели - не беда. Программа Вам сама предложит для всех элементов назначить материалом сталь. По окончании генерации Ваша модель будет выглядеть в виде сетки элементов. В моем случае модель стала состоять из чуть более 1 миллиона конечных элементов:

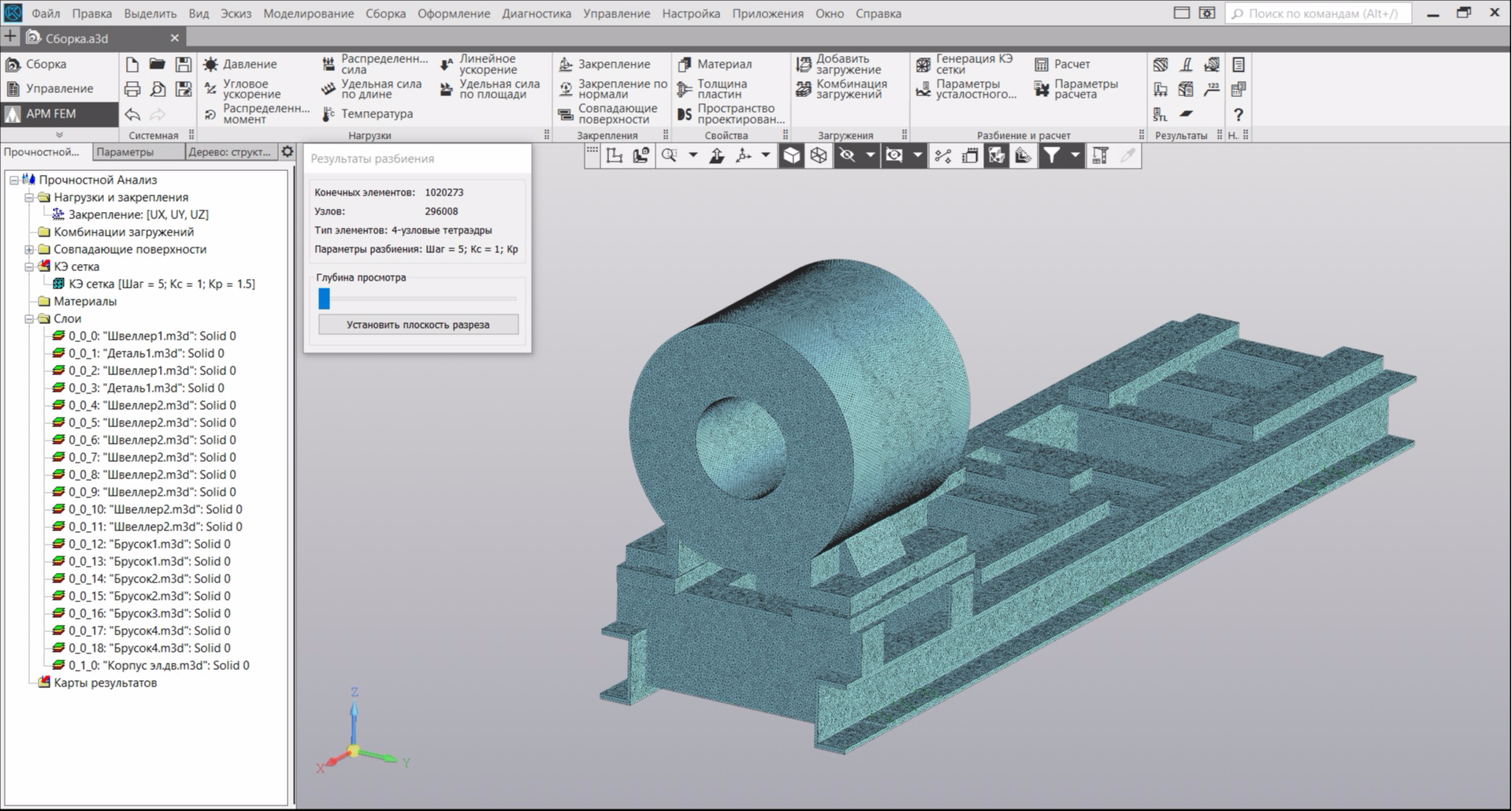
Далее, в панели, нажимаем кнопку "Расчет" и в диалоговом окне выбираем пункт "Собственные частоты":

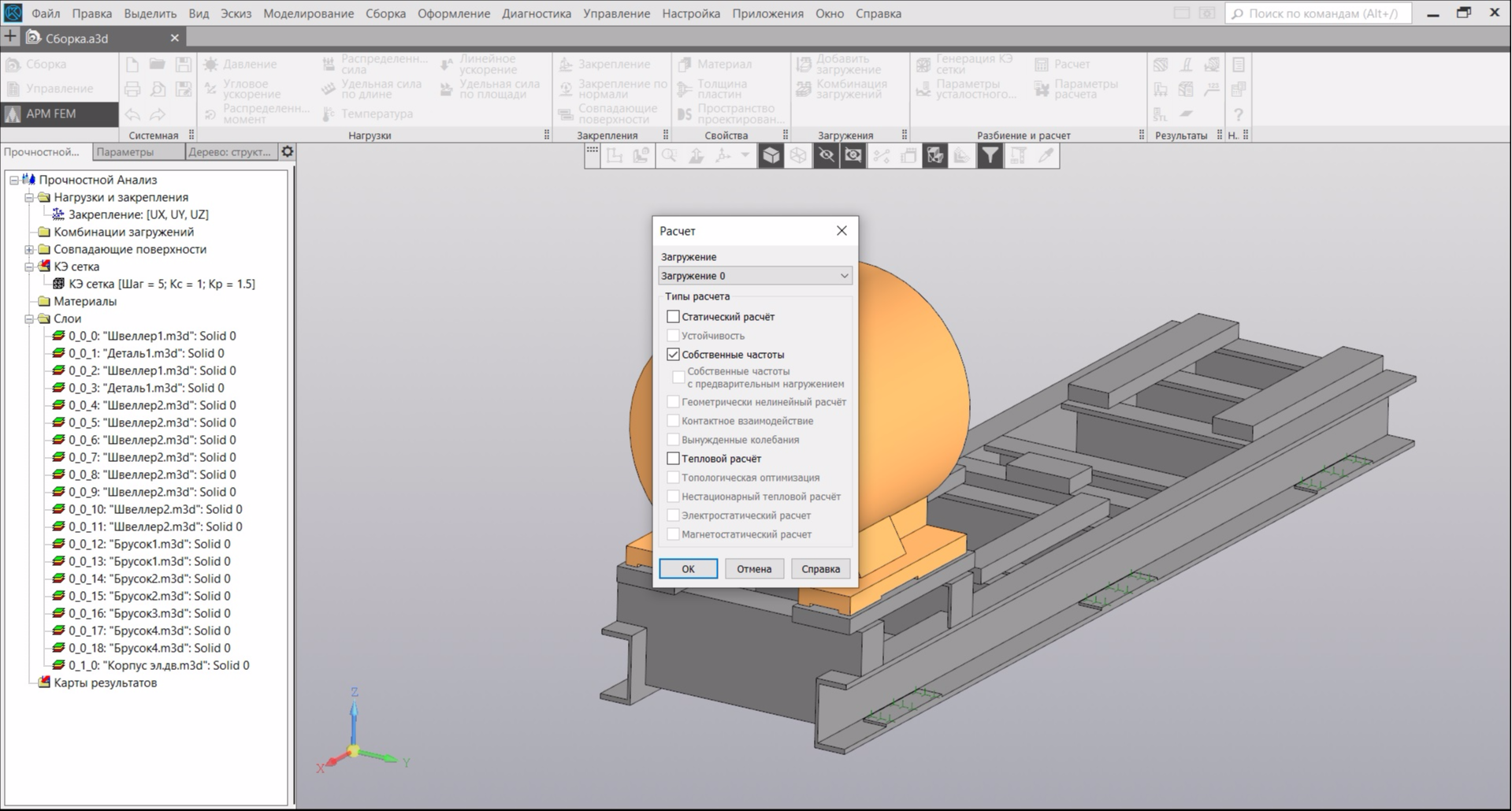
Можно идти пить кофе, так как расчет, в зависимости от выбранных параметров КЭ-сетки, занимает достаточно много времени. По окончании расчета нажимаем на иконку "Карта результатов" и раскрываем комбобокс "Частота". Программа выдаст нам таблицу с первыми пятью расчетными собственными частотами:

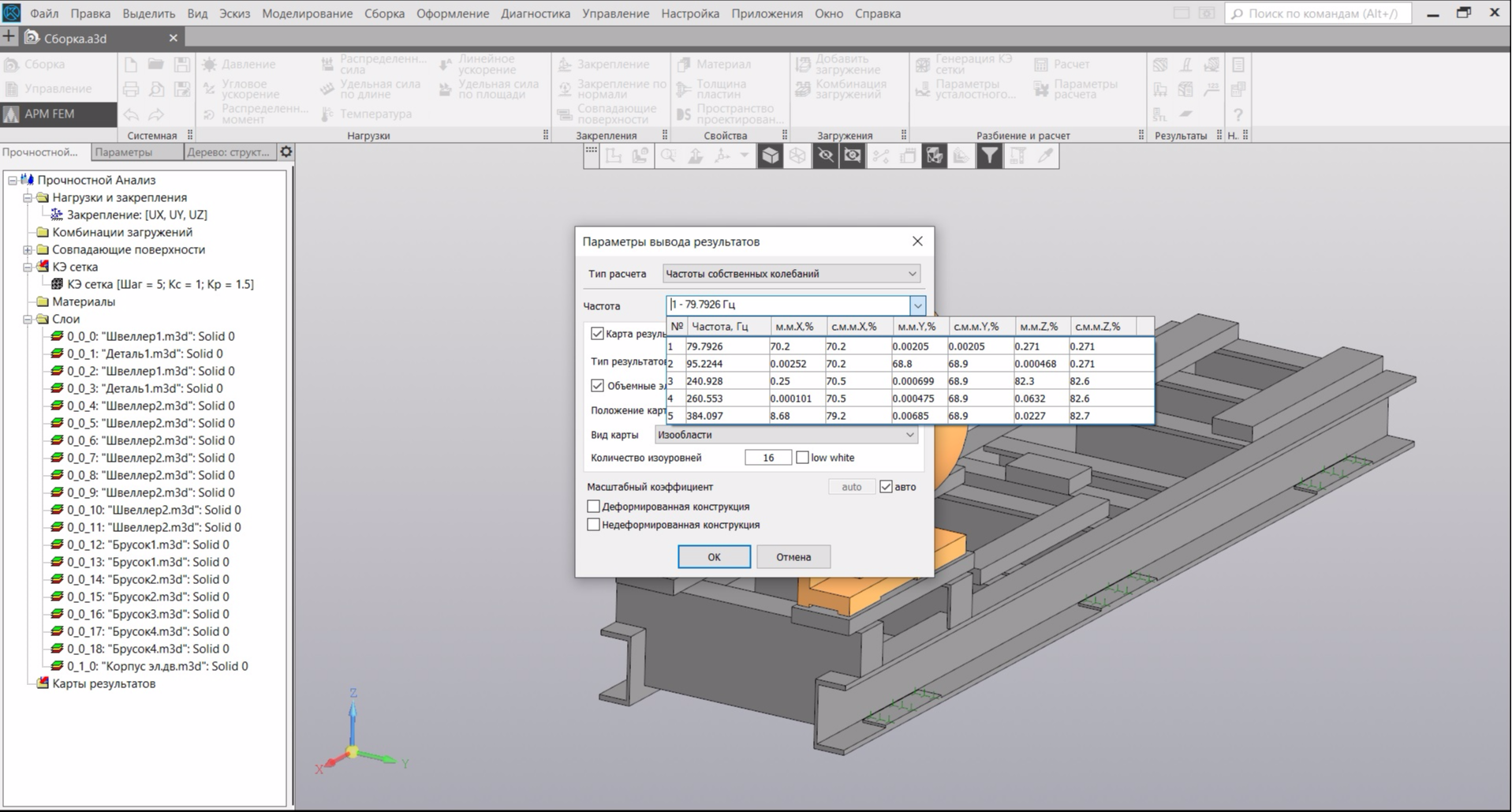
Но нас же еще интересует направление мод колебаний. Поэтому выбираем в таблице вторую строчку и жмем "ОК". В карте результатов появятся первые две моды колебаний (остальные нам не интересны), при выборе которых отобразится их визуальная картинка:

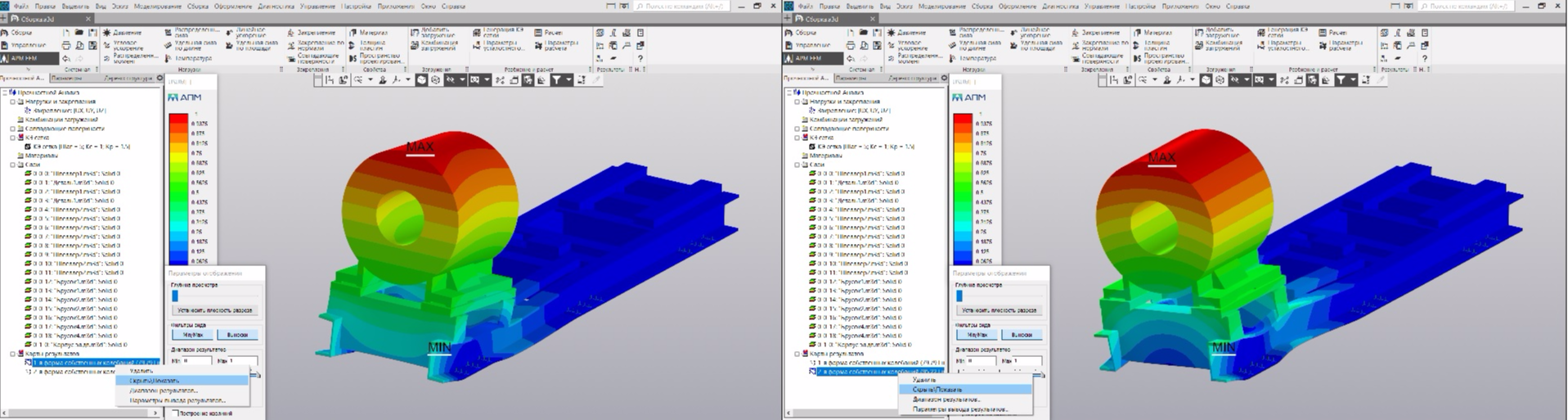
Слева - первая мода колебаний на частоте 79,79 Гц. Угадывается осевое направление колебаний. Реальная собственная частота в осевом направлении у нас была 78 Гц. Справа - вторая мода колебаний на частоте 95,22 Гц. Очень похоже на горизонтальное направление колебаний. Реальная собственная частота у нас составляла 98,7 Гц.

Реальные и расчетные данные у нас сходятся с незначительной погрешностью. Но вот с формами колебаний не очень понятно. Поэтому появилось желание воспользоваться зарекомендовавшим себя во всем мире инструментом проектировщиков - ANSYS. Никогда с этой программой не работал и вот появился повод.

Расчет в ANSYS

У меня нет желания рисовать модель заново, поэтому в Компас-3D сохраняю существующую модель в общем для обеих CAD-программ формате .igs. Далее открываем ANSYS Workbench. В панели инструментов (левая часть окна) находим систему анализа "Modal" и перетаскиваем ее на схему проекта (в центральную часть интерфейса). На схеме появится табличка:

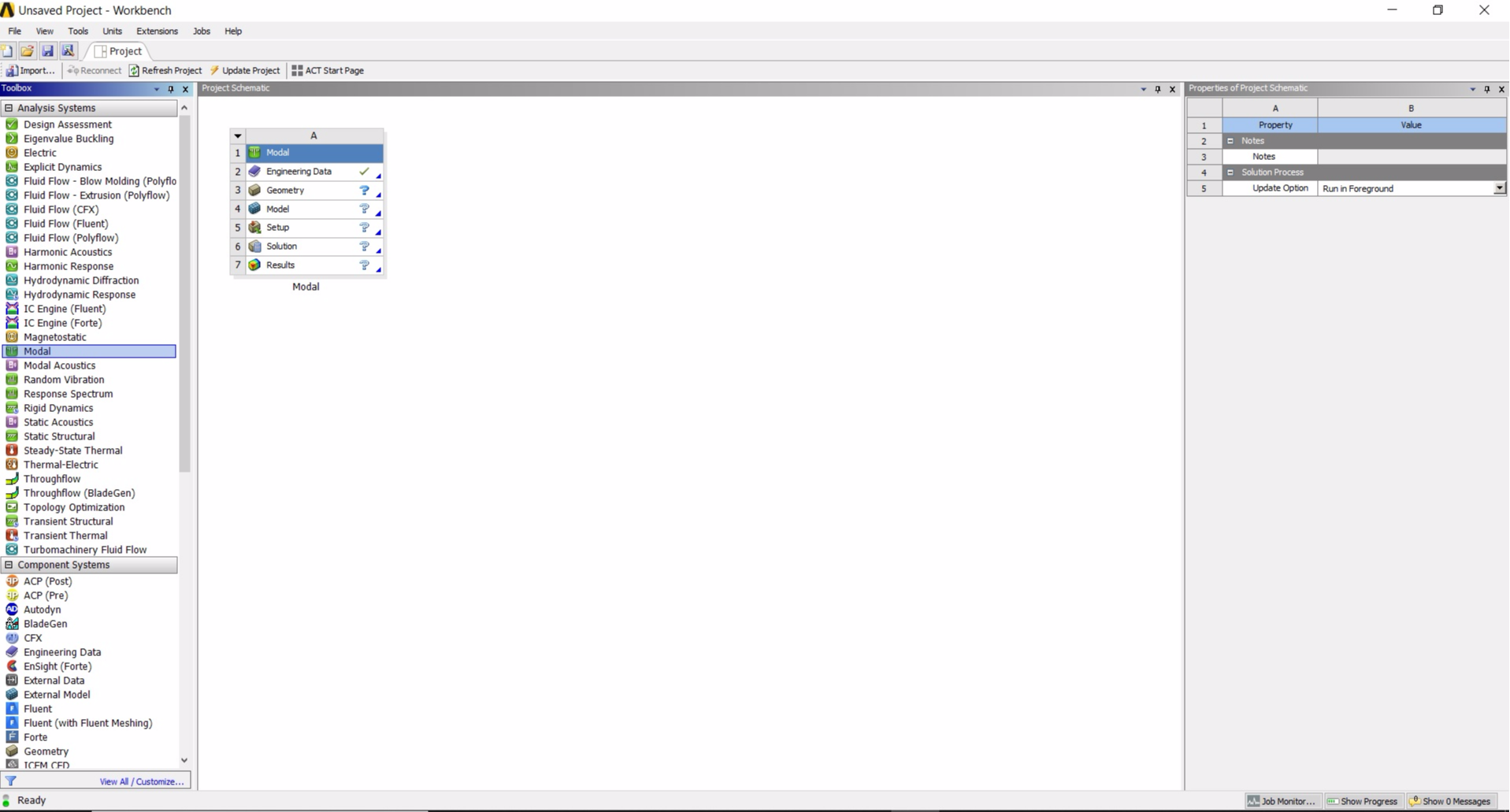
Первую строку таблицы "Modal" не трогаем. Вторая строка "Engineering Data" служит для выбора материалов, по умолчанию выбран только один материал для всех элементов модели - сталь. Этот материал нас полностью устраивает, но при необходимости щелкнув правой кнопкой мыши на эту строку и выбрав "Edit..." можно перейти к добавлению в набор других материалов. Третья строка "Geometry" служит для добавления геометрии модели в проект. Нажимаем правой кнопкой и в появившемся меню переходим "Import Geometry" → "Browse...", и выбираем ранее сохраненный файл в формате .igs. Наконец, четвертая интересная нам строка таблицы "Model". Жмем правой кнопкой и выбираем "Edit...". Запустится программа ANSYS Mechanical, в которой нам и предстоит работать дальше. Автоматически загрузится наша 3D-модель:

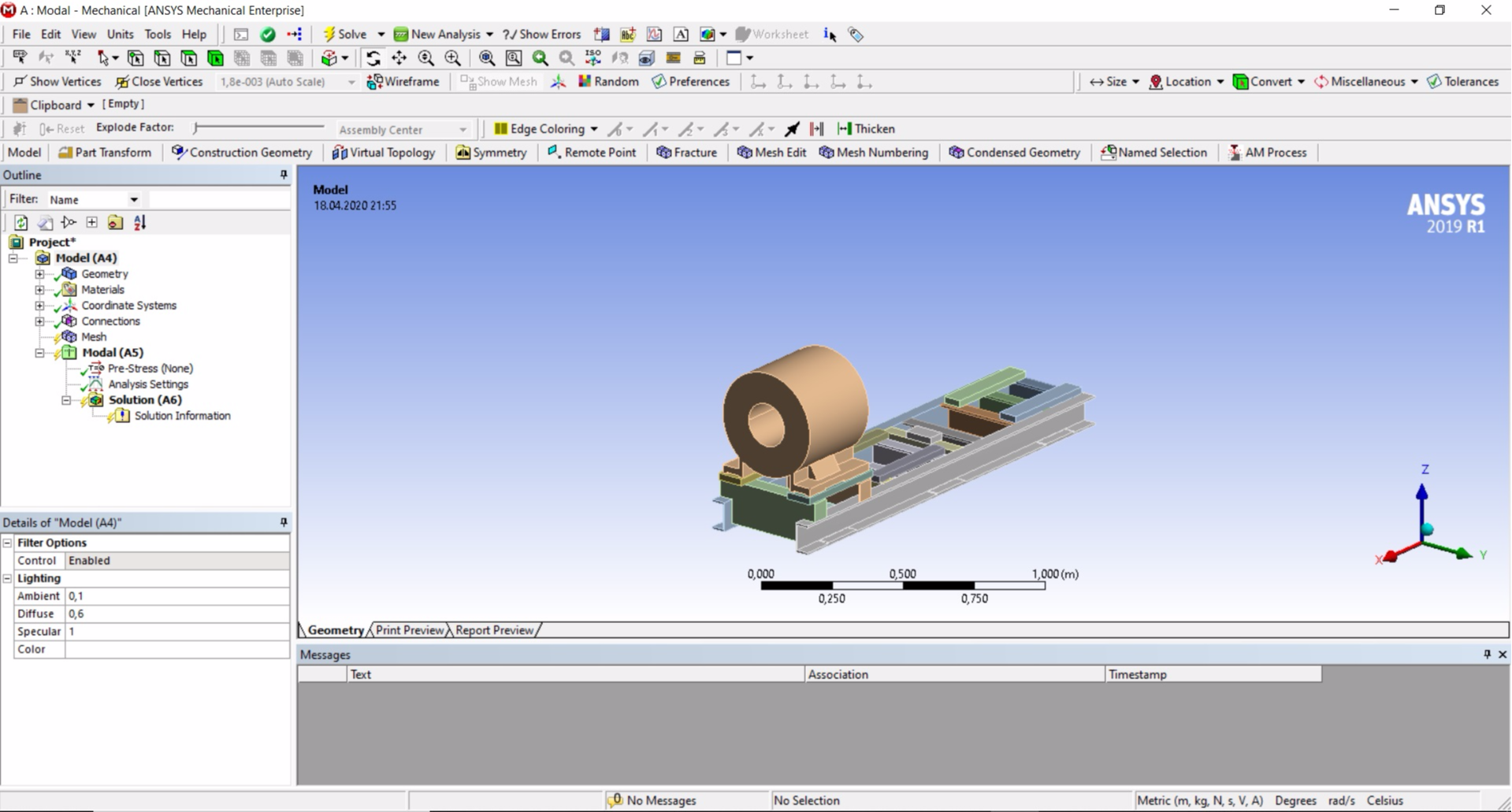
Далее необходимо выполнить несколько настроек. Во-первых, нам надо добавить места закрепления рамы. В дереве проекта жмем правой кнопкой мыши на "Analysis Settings", далее - "Insert" → "Fixed Support" и на модели выбираем места касания анкерных гаек к раме. После выбора поверхностей закрепления в левом нижнем углу экрана нажимаем "Apply".

Затем необходимо создать сетку конечных элементов. В дереве проекта выбираем "Mesh" и ниже в панели настроек раскрываем список "Sizing", находим и редактируем строку "Resolution". Выбираем значение 4. Это значение влияет на количество элементов в сетке. У кого оперативной памяти много, могут попробовать выбрать и более высокие значения. Далее правой кнопкой - "Mesh" → "Generate Mesh". Наша модель покроется необходимой нам сеткой.

Теперь необходимо задать количество мод колебаний, которые нам требуется рассчитать. Допустим, что нас интересуют первые пять мод. В дереве проектов выбираем "Analysis Settings" и в панели настроек ниже "Options" → "Max Modes to Find" устанавливаем значение 5. Затем в дереве проекта жмем правой кнопкой мыши на "Solution (A6)" и выбираем "Insert" → "Deformation" → "Total". В ветке "Solution (A6)" появится компонент "Total Deformation". Данную процедуру выполняем 5 раз. В эти компоненты пойдут результаты расчета мод колебаний. Каждому компоненту "Total Deformation" необходимо присвоить свою моду колебаний. Выбираем "Total Deformation 2" и в панели настроек ниже находим "Definition" → "Mode" и устанавливаем значение 2. Для "Total Deformation 3" устанавливаем значение 3 и так далее.

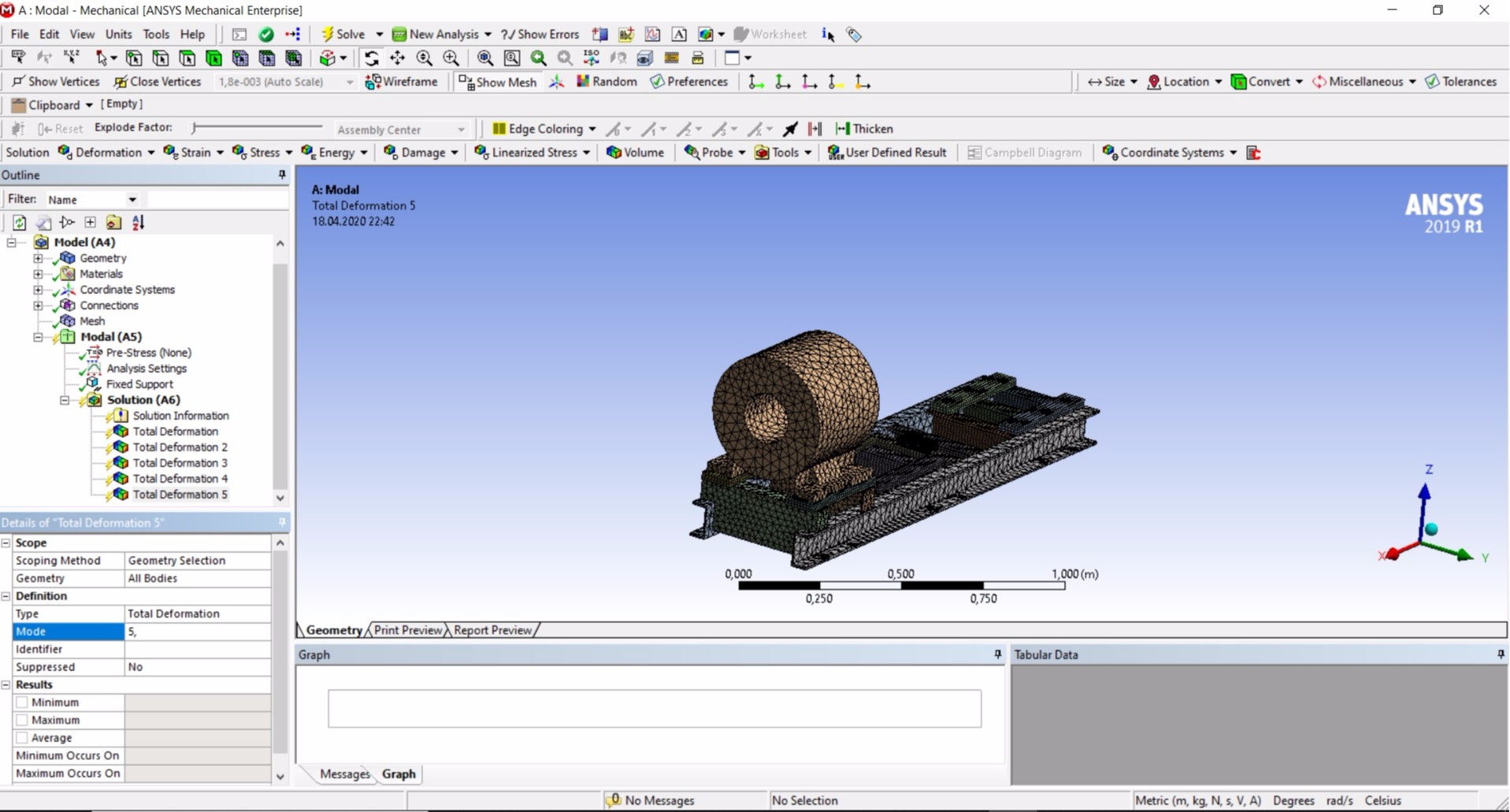
Все настройки завершены и для выполнения расчета нажимаем клавишу F5. Расчет потребует какого-то количества времени, и можно пойти попить кофе. Результаты расчета будут представлены в панелях снизу (под 3D-моделью):

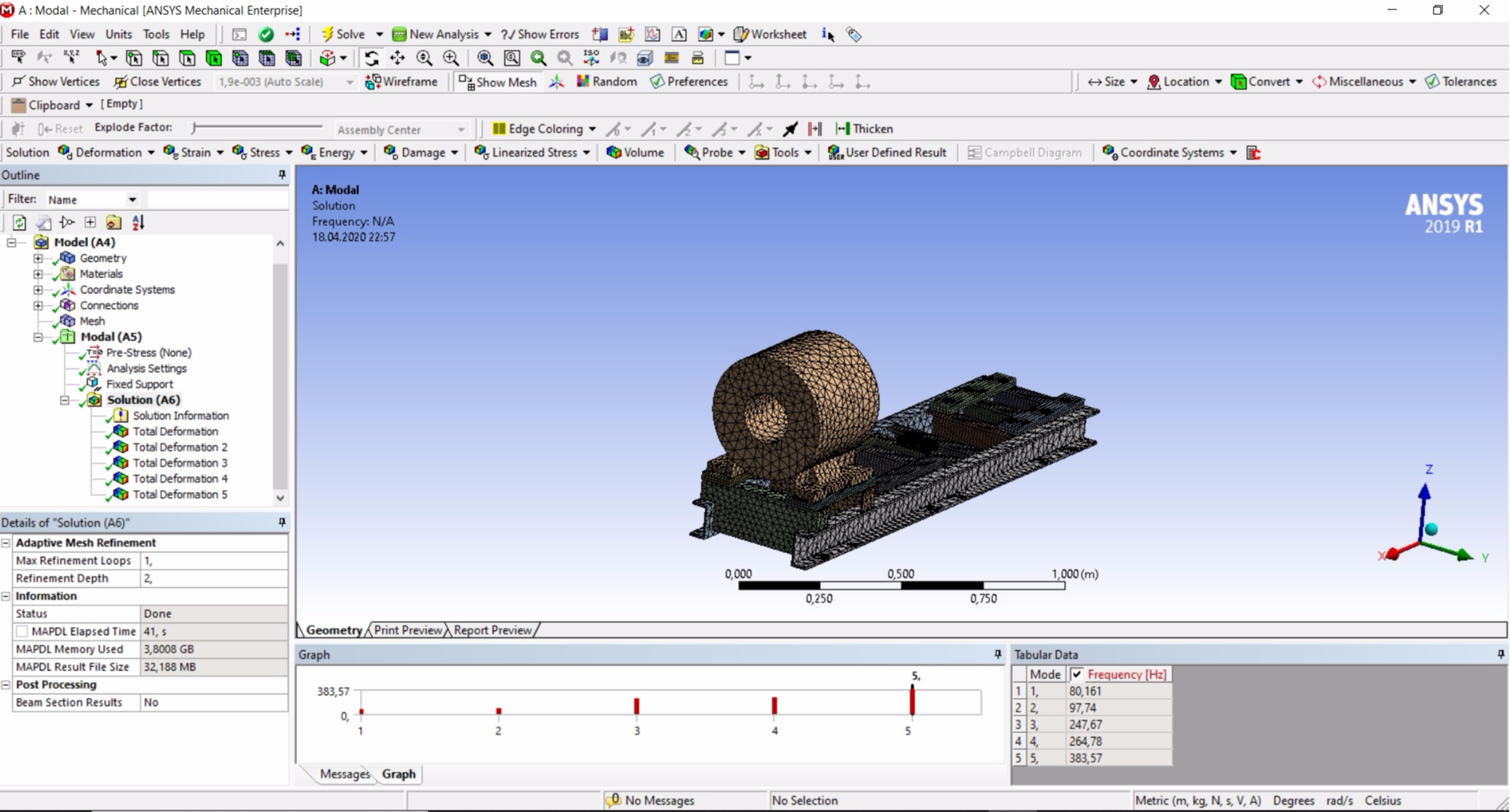
Первая мода колебаний на частоте 80,161 Гц, вторая мода - 97,74 Гц. Данные практически совпадают с реальными.

Для просмотра и воспроизведения каждой формы колебания необходимо нажать на соответствующий компонент "Total Deformation" в дереве проекта.

Вот так выглядит первая мода колебаний:

А вот так интересующие нас колебания по второй моде:

По визуализации проблемной второй моды колебаний видно, что в раме между анкерами происходят изгибные колебания. Причина - отсутствие прилегания к фундаменту. Получив эти данные, я пошел на место установки насоса, он как раз был в работе. Вибрация на нижней полке швеллера между анкерами более чем в 10 раз превышала вибрацию фундамента. Отсутствие прилегания подтвердилось. По всей видимости, заливка фундамента была выполнена некачественно.

Моделирование решения проблемы

Я более чем уверен, что владелец оборудования не будет перезаливать фундамент - проще оставить все как есть. Поэтому необходимо найти другой путь решения проблемы. Напрашиваются два варианта - монтаж дополнительных анкеров, либо установка пластин в пустоты между рамой и фундаментом.

Данные варианты должны увеличить жесткость и собственную частоту второй формы колебаний. Но насколько? Не забываем, что собственная частота по первой форме 78 Гц, и нам крайне не желательно увеличить ее до 100 Гц и получить резонанс в осевом направлении. Поэтому попробуем хоть как-то смоделировать оба варианта установкой небольших пластин между рамой и фундаментом, добавив закрепление по ним.

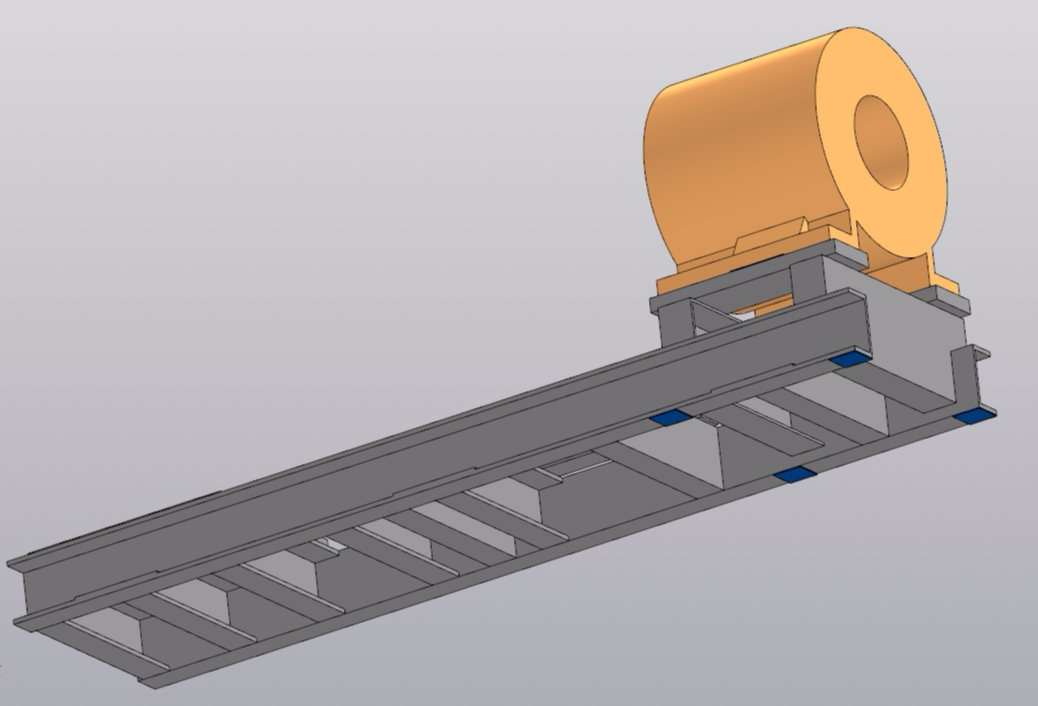
Расчет в APM FEM

Результаты расчета в Компас-3D:

Визуализация первых двух мод:

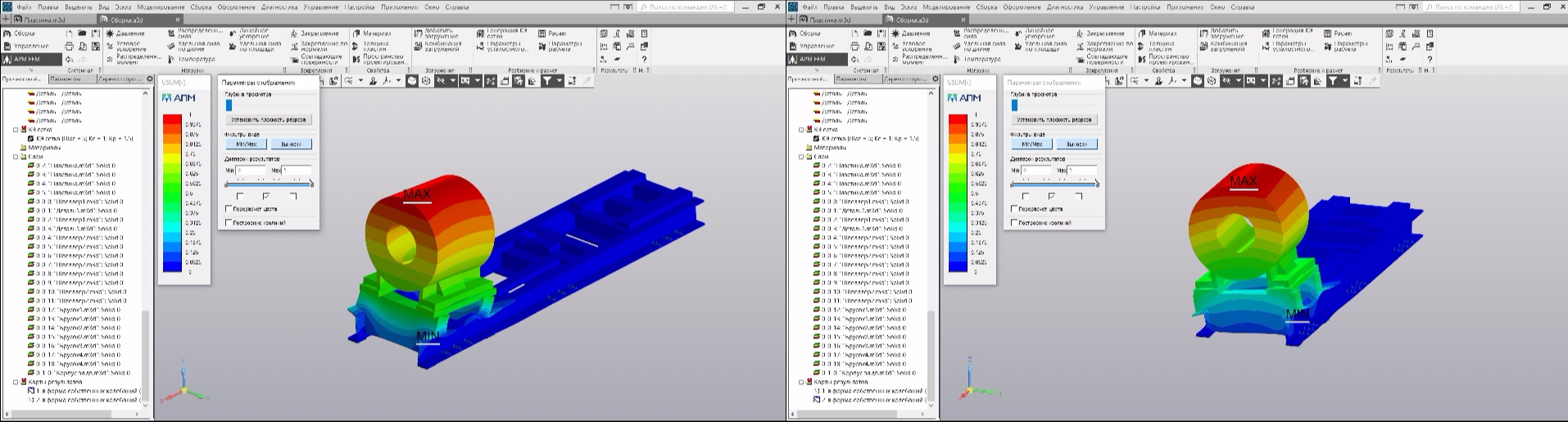
Как видим, направления колебаний певрой (слева) и второй (справа) мод остались прежними.

Расчет в ANSYS

Результаты расчета:

Визуализация первой моды колебаний:

И вторая мода:

Заключение

Результаты расчетов в Компас-3D и ANSYS схожи, можно пользоваться любым из этих инструментов. Поскольку скорость расчета и визуализация в ANSYS лучше, рекомендую использовать последний.

Недостатком моделирования мод колебаний является высокая времязатратность. Снятие размеров по месту эксплуатации у меня заняло 40 минут, создание 3D-модели - около 4 часов, расчет в AMP FEM - 1 час, расчет в ANSYS - 30 минут.

Преимущество - визуализация колебаний конструкции, возможность быстро смоделировать варианты решения проблем.

Как итог, модальный анализ подтвердил наличие структурного резонанса и помог идентифицировать коренную причину. Дальнейшее моделирование показало, что усиление прилегания рамы под электродвигателем должно отстроить собственные частоты конструкции от двойной частоты сети 100 Гц и избавить электродвигатель от резонанса. Результаты этой работы будут переданы владельцу оборудования. Очень надеюсь, что в скором времени я смогу порадовать Вас статьей об итогах запланированных работ.