May 27, 2020, 9:31 p.m.

Разработка программы многоплоскостной балансировки

Здравствуйте, друзья! Пришла пора заняться чем-то полезным, а конкретно - разработать ПО для балансировки на ПК и смартфон. К сожалению, хороших бесплатных программ я не нашел, а ПО в приборах имеют свои недостатки. Поэтому, предлагаю восполнить этот пробел.

Цель - возможность многоплоскостной балансировки по месту эксплуатации с хорошим качеством и визуализацией (контролем). Поскольку это дело сложное, то разработку планирую разбить на три основных этапа:
1. Отработка основных алгоритмов в консольном приложении (Qt/C++);
2. Написание ПО на десктоп (QML/JS);
3. Портирование ПО на Android.

В данной теме Вы сможете наблюдать весь процесс разработки (если интересно), а при желании и помогать. Любая Ваша помощь, критика и советы будут очень востребованы. Исходный код и само ПО будут открыты и бесплатны. Сроки обозначить не могу - свободного времени не так уж и много. Поэтому как только, так сразу.

Subscribers

  • 5066
  • 0
  • 0
  • 0
20

Для балансировочных расчетов воспользуемся алгоритмом из данного учебного пособия, немного модернизировав его. В общем виде он будет следующим:
1. Расчет уравновешивающих масс и остаточных вибраций.
2. Выравнивание остаточных вибраций (опционально) и перерасчет уравновешивающих масс.
3. Установка нерасчетных масс и вычисление ожидаемых остаточных вибраций.
4. Расчет уравновешивающих масс и остаточных вибраций в случае несоответствия реальных остатков вибраций ожидаемым с использованием матрицы невязок.
5. Повторение п.2 и п.3.

  • 0
  • 0
  • 0

На данный момент выкладываю исходный код консольной программы по пунктам 1-3.

Исходный код 
#include <QCoreApplication>
#include <QTextStream>
#include <QDebug>
#include <QtMath>
#include <QVector>
QTextStream cout(stdout);
QTextStream cin(stdin);
// Функция транспонирования массива
QVector<QVector<qreal>> transposeMatrix(QVector<QVector<qreal>> A, int n, int k){
    QVector<qreal> line(k, 0);
    QVector<QVector<qreal>> B(n,line);
    for(int j = 0; j < k; j++){
        for(int i = 0; i < n; i++){
            B[i][j] = A[j][i];
        }
    }
    return B;
}
// Функция умножения двухмерных матриц
QVector<QVector<qreal>> multiplicationMatrix(QVector<QVector<qreal>> A, QVector<QVector<qreal>> B, int n, int m, int l){
    QVector<qreal> line(m, 0);
    QVector<QVector<qreal>> C(n,line);
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < m; j++)
        {
            for (int k = 0; k < l; k++)
                C[i][j] += A[i][k] * B[k][j];
        }
    }
    return C;
}
// Функция умножения двухмерной матрицы на одномерную
QVector<qreal> multiplicationMatrix2(QVector<QVector<qreal>> A, QVector<qreal> B, int n, int m){
    QVector<qreal> C(n);
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < m; j++)
        {
            C[i] += A[i][j] * B[j];
        }
    }
    return C;
}
// Функция вычисления обратной матрицы
void calculateInverse(QVector<QVector<qreal>>& A) {
    int n = A.size();
    for (int i=0; i<n; i++) {
        // Ищем максимум в этом столбце
        double maxEl = abs(A[i][i]);
        int maxRow = i;
        for (int k=i+1; k<n; k++) {
            if (abs(A[k][i]) > maxEl) {
                maxEl = A[k][i];
                maxRow = k;
            }
        }
        // Меняем местами максимальную строку с текущей строкой (столбец за столбцом)
        for (int k=i; k<2*n;k++) {
            double tmp = A[maxRow][k];
            A[maxRow][k] = A[i][k];
            A[i][k] = tmp;
        }
        // Обнуляем последующие строки в текущем столбце
        for (int k=i+1; k<n; k++) {
            double c = -A[k][i]/A[i][i];
            for (int j=i; j<2*n; j++) {
                if (i==j) {
                    A[k][j] = 0;
                } else {
                    A[k][j] += c * A[i][j];
                }
            }
        }
    }
    // Решаем уравнение Ax = b для верхней треугольной матрицы A
    for (int i=n-1; i>=0; i--) {
        for (int k=n; k<2*n;k++) {
            A[i][k] /= A[i][i];
        }
        // В этом нет необходимости, но результат выглядит лучше:
        A[i][i] = 1;
        for (int rowModify=i-1;rowModify>=0; rowModify--) {
            for (int columModify=n;columModify<2*n;columModify++) {
                A[rowModify][columModify] -= A[i][columModify]
                        * A[rowModify][i];
            }
            // В этом нет необходимости, но результат выглядит лучше:
            A[rowModify][i] = 0;
        }
    }
}
// Функция внесения минуса в матрицу
QVector<QVector<qreal>> minusToMatrix(QVector<QVector<qreal>> A, int n){
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
            A[i][j] = -A[i][j];
    }
    return A;
}

int main(int argc, char *argv[])
{
    setlocale(LC_ALL,"Russian");
    QCoreApplication a(argc, argv);
    int number_points; // Количество точек измерений
    int number_planes; // Количество балансировочных плоскостей
    qDebug() << "Введите количество точек измерений:";
    cin >> number_points;
    qDebug() << "Введите количество балансировочных плоскостей:";
    cin >> number_planes;
    qDebug() << "Введите амплитуду/фазу нулевого пуска (исходная вибрация):";
    QVector<qreal> sensitivity(2*number_points); //обобщенные чувствительности (понадобится в дальнейшем)
    // Заполняем массивы амплитуды и фазы данными 0 пуска
    QVector<qreal> ampl(number_points); // Массив амплитуд 0 пуска
    QVector<qreal> phase(number_points); // Массив фаз 0 пуска
    for(int i = 0; i < number_points; i++){
        cin >> ampl[i];
        cin >> phase[i];
    }
    qDebug() << "Амплитуды" << ampl;
    qDebug() << "Фазы" << phase;
    QVector<qreal> ampl_projections(2*number_points); // Массив проекций на оси X и Y
    int k = 0;
    for(int i = 0; i < number_points; i++){
        ampl_projections[k] = ampl[i]*qCos(qDegreesToRadians(phase[i]));
        ampl_projections[k+1] = ampl[i]*qSin(qDegreesToRadians(phase[i]));
        k = k + 2;
    }
    qDebug() << "Проекции: " << ampl_projections;
    // Данные пробных балансировочных пусков
    QVector<qreal> weight(number_planes); // Массив масс грузов
    QVector<qreal> alpha(number_planes); // Массив углов установки грузов
    QVector<qreal> line1(number_planes, 0);
    QVector<QVector<qreal>> ampl2(number_points, line1); // Массив амплитуд пусков с пробными грузами
    QVector<QVector<qreal>> phase2(number_points, line1); // Массив фаз пусков с пробными грузами
    for(int j = 0; j < number_planes; j++){
        qDebug() << "Пуск №" << j+1 << ":";
        qDebug() << "Введите массу пробного груза, установленного в плоскости №" << j+1 << ":";
        cin >> weight[j];
        qDebug() << "Введите угол установки пробного груза, установленного в плоскости №" << j+1 << ":";
        cin >> alpha[j];
        qDebug() << "Введите амплитуду/фазу пробного пуска №" << j+1 << ":";
        for(int i = 0; i < number_points; i++){
            cin >> ampl2[i][j];
            cin >> phase2[i][j];
        }
    }
    qDebug() << "Амплитуды" << ampl2;
    qDebug() << "Фазы" << phase2;
    // Матрица чувствительностей при нормировании к единичным массам
    QVector<qreal> line2(2*number_planes, 0);
    QVector<QVector<qreal>> a_projections2(2*number_points,line2); // Массив проекций векторов влияния на оси X и Y (в соответствии с алгоритмом)
    int row;
    int col=0;
    for(int j = 0; j < number_planes; j++){
        row = 0;
        for(int i = 0; i < number_points; i++){
            a_projections2[row][col] = round(((ampl2[i][j]*qCos(qDegreesToRadians(phase2[i][j])) - ampl_projections[row])*weight[j]*
                                              qCos(qDegreesToRadians(alpha[j])) + (ampl2[i][j]*qSin(qDegreesToRadians(phase2[i][j])) - ampl_projections[row+1])*weight[j]*
                                             qSin(qDegreesToRadians(alpha[j])))/(weight[j]*weight[j])*1000000)/1000000;
            a_projections2[row+1][col] = round(((ampl2[i][j]*qSin(qDegreesToRadians(phase2[i][j])) - ampl_projections[row+1])*weight[j]*
                                               qCos(qDegreesToRadians(alpha[j])) - (ampl2[i][j]*qCos(qDegreesToRadians(phase2[i][j])) - ampl_projections[row])*weight[j]*
                                               qSin(qDegreesToRadians(alpha[j])))/(weight[j]*weight[j])*1000000)/1000000;
            a_projections2[row][col+1] = a_projections2[row+1][col]*(-1);
            a_projections2[row+1][col+1] = a_projections2[row][col];
            row = row + 2;
        }
        col = col + 2;
    }
    qDebug() << "Матрица чувствительностей: " << a_projections2;
    QVector<qreal> line3(2*number_points, 0);
    QVector<QVector<qreal>> a_projections2_t(2*number_planes,line3); // Транспонированный массив a_projections2[][]
    a_projections2_t = transposeMatrix(a_projections2, 2*number_planes, 2*number_points);
    qDebug() << "Транспонированная матрица чувствительностей: " << a_projections2_t;
    QVector<QVector<qreal>> A(2*number_planes,line2);
    A = multiplicationMatrix(a_projections2_t, a_projections2, 2*number_planes, 2*number_planes, 2*number_points);
    qDebug() << "Матрица А: " << A;
    // Расчет обратной матрицы
    // Входные данные
    QVector<qreal> line4(4*number_planes,0);
    QVector<QVector<qreal>> A2(2*number_planes,line4);
    // Передаем в вектор А2 массив a_projections2_x[][]
    for (int i=0; i<2*number_planes; i++) {
        for (int j=0; j<2*number_planes; j++) {
            A2[i][j] = A[i][j];
        }
    }
    // Дополняем матрицу диагональю единичек (требует метод расчета обратной матрицы)
    for (int i=0; i<2*number_planes; i++) {
        A2[i][2*number_planes+i] = 1;
    }
    calculateInverse(A2);
    qDebug() << "Обратная матрица А2: " << A2;
    // Удаляем добавочные столбцы
    QVector<QVector<qreal>> B(2*number_planes,line2); // Массив обратной матрицы
    for (int i = 0; i < 2*number_planes; i++)
    {
        for (int j = 0; j < 2*number_planes; j++)
            B[i][j]=A2[i][j+2*number_planes];
    }
    // В соответствии с алгоритмом вносим минус в обратную матрицу
    QVector<QVector<qreal>> C(2*number_planes,line2); // Mатрица -B[][]
    C = minusToMatrix(B, 2*number_planes);
    // Умножаем все это дело на транспонированную матрицу проекций
    QVector<QVector<qreal>> D(2*number_planes,line3); // Промежуточная матрица умножения
    D = multiplicationMatrix(C, a_projections2_t, 2*number_planes, 2*number_points, 2*number_planes);
    qDebug() << "Матрица D: " << D;
    // И умножаем на исходную матрицу вибраций - получаем матрицу весов
    QVector<qreal> weights_matrix(2*number_planes); // Матрица весов
    weights_matrix = multiplicationMatrix2(D, ampl_projections, 2*number_planes, 2*number_points);
    qDebug() << "Матрица weights_matrix: " << weights_matrix;
    // Вычисление величин и положений уравновешивающих масс
    qDebug() << "Расчетное положение балансировочных грузов:";
    QVector<qreal> cargo_weight(number_planes); // Массив масс расчетных балансировочных грузов
    QVector<qreal> cargo_phi(number_planes); // Массив углов установки балансировочных грузов
    int l = 0;
    for(int i = 0; i<number_planes; i++){
        cargo_weight[i] = sqrt(weights_matrix[l]*weights_matrix[l] + weights_matrix[l+1]*weights_matrix[l+1]);
        if(weights_matrix[l] >= 0){
            cargo_phi[i] = qAtan(weights_matrix[l+1]/weights_matrix[l])*180/M_PI;
        } else {
            cargo_phi[i] = (qAtan(weights_matrix[l+1]/weights_matrix[l])*180/M_PI + 180);
        }
        qDebug() << "Плоскость №"<< i+1 << ":";
        qDebug() << "Масса = "<< cargo_weight[i] << ", " << "Угол = "<< cargo_phi[i];
        l = l + 2;
    }
    // Далее необходимо вычислить остаточную вибрацию после установки расчетных грузов
    // Умножаем матрицу проекций на матрицу весов
    QVector<qreal> E(2*number_points); // Промежуточный массив
    for (int i = 0; i < 2*number_points; i++)
    {
        for (int j = 0; j < 2*number_planes; j++){
            E[i] += a_projections2[i][j]*weights_matrix[j];
        }
    }
    // Матрица остаточных уровней вибрации
    QVector<qreal> F(2*number_points); // Массив проекций остаточных вибраций
    for(int i=0; i<2*number_points; i++){
        F[i] = E[i] + ampl_projections[i];
    }
    // Амплитуда и фаза остаточных уровней вибрации (перевод из декартовых координат в полярные)
    qDebug() << "Остаточные вибрации:";
    QVector<qreal> residual_ampl(number_points); // Массив амплитуд
    QVector<qreal> residual_phi(number_points); // Массив фаз
    int m = 0;
    for(int i = 0; i<number_points; i++){
        residual_ampl[i] = sqrt(F[m]*F[m] + F[m+1]*F[m+1]);
        if(F[m] >= 0){
            residual_phi[i] = qAtan(F[m+1]/F[m])*180/M_PI;
        } else {
            residual_phi[i] = qAtan(F[m+1]/F[m])*180/M_PI + 180;
        }
        // Вывод остаточных вибраций
        qDebug() << "Точка "<< i+1 << ":";
        qDebug() << "Амплитуда/Фаза "<< residual_ampl[i] << "/" << residual_phi[i];
        m = m + 2;
    }
    //////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
    int equation;
    qDebug() << "Нужно ли выравнивание остаточных вибраций? (0 - да, 1 - нет):";
    cin >> equation;
    if(equation == 0){
        // Далее выполним выравнивание остаточных вибраций (минимизируем максимальные)
        qDebug() << "Выравнивание остаточных вибраций:";
        qreal rms; // СКЗ остаточных вибраций по всем точкам контроля
        qreal g_sum = 0; // Сумма остаточных вибраций по всем точкам контроля
        for(int i = 0; i < number_points; i++){
            g_sum += residual_ampl[i];
        }
        qDebug() << "g_sum:" << g_sum;
        rms = sqrt(g_sum/number_points);
        qDebug() << "rms:" << rms;
        QVector<qreal> G(number_points); // Массив взвешивающих коэффициентов для всех точек контроля
        for(int i = 0; i < number_points; i++){
            G[i] = residual_ampl[i]/rms;
        }
        qDebug() << "G:" << G;
        // Умножаем последовательно пары столбцов a_projections2_t[2*number_planes][2*number_points] на G[i]
        QVector<QVector<qreal>> H(2*number_planes,line3); // Транспонированная матрица чувствительностей со взвешивающими коэффициентами
        for(int i = 0; i < 2*number_planes; i++){
            k = 0;
            for(int j = 0; j < number_points; j++){
                H[i][k] = a_projections2_t[i][k]*G[j];
                H[i][k+1] = a_projections2_t[i][k+1]*G[j];
                k = k + 2;
            }
        }
        qDebug() << "H:" << H;
        // Вычисляем матрицу скорректированных значений уравновешивающих масс
        // Умножаем транспонированную матрицу чувствительностей со взвешивающими коэффициентами на матрицу проекций
        QVector<QVector<qreal>> I(2*number_planes,line2); // Массив произведения T[][] x a_projections2[][]
        I = multiplicationMatrix(H, a_projections2, 2*number_planes, 2*number_planes, 2*number_points);
        qDebug() << "I:" << I;
        // Расчет обратной матрицы I[][]
        QVector<QVector<qreal>> I2(2*number_planes,line4);
        // Передаем в вектор I массив I2[][]
        for (int i=0; i<2*number_planes; i++) {
            for (int j=0; j<2*number_planes; j++) {
                I2[i][j] = I[i][j];
            }
        }
        qDebug() << "I2:" << I2;
        // Дополняем матрицу диагональю единичек (требует метод расчета обратной матрицы)
        for (int i=0; i<2*number_planes; i++) {
            I2[i][2*number_planes+i] = 1;
        }
        // Передаем исходную матрицу в функцию расчета
        calculateInverse(I2);
        qDebug() << "I2:" << I2;
        QVector<QVector<qreal>> K(2*number_planes,line2); // Массив обратной матрицы
        for (int i = 0; i < 2*number_planes; i++)
        {
            for (int j = 0; j < 2*number_planes; j++)
                K[i][j]=I2[i][j+2*number_planes];
        }
        qDebug() << "K:" << K;
        // В соответствии с алгоритмом вносим минус в обратную матрицу
        QVector<QVector<qreal>> L(2*number_planes,line2); // Mатрица -K[][]
        L = minusToMatrix(K, 2*number_planes);
        qDebug() << "L:" << L;
        // Умножаем все это дело на транспонированную матрицу проекций (в соответствии с алгоритмом)
        QVector<QVector<qreal>> M(2*number_planes,line3); // Промежуточный массив
        M = multiplicationMatrix(L, H, 2*number_planes, 2*number_points, 2*number_planes);
        qDebug() << "M:" << M;
        // И умножаем на исходную матрицу вибраций - получаем матрицу весов
        QVector<qreal> weights_matrix2(2*number_planes); // Матрица весов
        weights_matrix2 = multiplicationMatrix2(M, ampl_projections, 2*number_planes, 2*number_points);
        qDebug() << "Матрица weights_matrix2: " << weights_matrix2;
        // Вычисление величин и положений уравновешивающих масс
        qDebug() << "Новое расчетное положение балансировочных грузов:";
        QVector<qreal> cargo_weight2(number_planes); // Массив масс расчетных балансировочных грузов
        QVector<qreal> cargo_phi2(number_planes); // Массив углов установки балансировочных грузов
        int l = 0;
        for(int i = 0; i<number_planes; i++){
            cargo_weight2[i] = sqrt(weights_matrix2[l]*weights_matrix2[l] + weights_matrix2[l+1]*weights_matrix2[l+1]);
            if(weights_matrix2[l] >= 0){
                cargo_phi2[i] = qAtan(weights_matrix2[l+1]/weights_matrix2[l])*180/M_PI;
            } else {
                cargo_phi2[i] = (qAtan(weights_matrix2[l+1]/weights_matrix2[l])*180/M_PI + 180);
            }
            qDebug() << "Плоскость №"<< i+1 << ":";
            qDebug() << "Масса = "<< cargo_weight2[i] << ", " << "Угол = "<< cargo_phi2[i];
            l = l + 2;
        }
        // Далее необходимо вычислить остаточную вибрацию после установки расчетных грузов
        // Умножаем матрицу проекций на матрицу весов
        QVector<qreal> E2(2*number_points); // Промежуточный массив
        for (int i = 0; i < 2*number_points; i++)
        {
            for (int j = 0; j < 2*number_planes; j++){
                E2[i] += a_projections2[i][j]*weights_matrix2[j];
            }
        }
        // Матрица остаточных уровней вибрации
        QVector<qreal> F2(2*number_points); // Массив проекций остаточных вибраций
        for(int i=0; i<2*number_points; i++){
            F2[i] = E2[i] + ampl_projections[i];
        }
        // Амплитуда и фаза остаточных уровней вибрации (перевод из декартовых координат в полярные)
        qDebug() << "Новые остаточные вибрации:";
        QVector<qreal> residual_ampl2(number_points); // Массив амплитуд
        QVector<qreal> residual_phi2(number_points); // Массив фаз
        m = 0;
        for(int i = 0; i<number_points; i++){
            residual_ampl2[i] = sqrt(F2[m]*F2[m] + F2[m+1]*F2[m+1]);
            if(F2[m] >= 0){
                residual_phi2[i] = qAtan(F2[m+1]/F2[m])*180/M_PI;
            } else {
                residual_phi2[i] = qAtan(F2[m+1]/F2[m])*180/M_PI + 180;
            }
            // Вывод остаточных вибраций
            qDebug() << "Точка "<< i+1 << ":";
            qDebug() << "Амплитуда/Фаза "<< residual_ampl2[i] << "/" << residual_phi2[i];
            m = m + 2;
        }
        // Расчет обобщенных чувствительностей
        for(int i = 0; i < 2*number_points; i++){
            sensitivity[i] = F2[i] - ampl_projections[i];
        }
    }
    if(equation == 1){
        for(int i = 0; i < 2*number_points; i++){
            sensitivity[i] = F[i] - ampl_projections[i];
        }
    }
    QVector<qreal> sensitivity_ampl(number_points);
    QVector<qreal> sensitivity_phi(number_points);
    m = 0;
    for(int i = 0; i<number_points; i++){
        sensitivity_ampl[i] = sqrt(sensitivity[m]*sensitivity[m] + sensitivity[m+1]*sensitivity[m+1]);
        if(sensitivity[m] >= 0){
            sensitivity_phi[i] = qAtan(sensitivity[m+1]/sensitivity[m])*180/M_PI;
        } else {
            sensitivity_phi[i] = qAtan(sensitivity[m+1]/sensitivity[m])*180/M_PI + 180;
        }
        // Вывод остаточных вибраций
        qDebug() << "Точка "<< i+1 << ":";
        qDebug() << "Чувствительность "<< sensitivity_ampl[i] << "/" << sensitivity_phi[i];
        m = m + 2;
    }
    //////////////////////////////////////////////////////////////////////////////////////////////////////
    // Установка масс
    qDebug() << "Установка масс:";
    QVector<qreal> cargo_weight3(number_planes);
    QVector<qreal> cargo_phi3(number_planes);
    for(int i = 0; i < number_planes; i++){
        qDebug() << "В плоскости "<< i+1 << ":";
        qDebug() << "Масса:";
        cin >> cargo_weight3[i];
        qDebug() << "Угол:";
        cin >> cargo_phi3[i];
    }
    // Раскладываем на проекции и записываем в матрицу весов
    QVector<qreal> weights_matrix3(2*number_planes);
    m = 0;
    for(int i = 0; i < number_planes; i++){
        weights_matrix3[m] = cargo_weight3[i]*qCos(qDegreesToRadians(cargo_phi3[i]));
        weights_matrix3[m+1] = cargo_weight3[i]*qSin(qDegreesToRadians(cargo_phi3[i]));
        m = m + 2;
    }
    qDebug() << "weights_matrix3:"<< weights_matrix3;
    // Далее необходимо вычислить остаточную вибрацию после установки реальных грузов
    // Умножаем матрицу проекций на матрицу весов
    QVector<qreal> E3(2*number_points); // Промежуточный массив
    for (int i = 0; i < 2*number_points; i++)
    {
        for (int j = 0; j < 2*number_planes; j++){
            E3[i] += a_projections2[i][j]*weights_matrix3[j];
        }
    }
    // Матрица остаточных уровней вибрации
    QVector<qreal> F3(2*number_points); // Массив проекций остаточных вибраций
    for(int i=0; i<2*number_points; i++){
        F3[i] = E3[i] + ampl_projections[i];
    }
    // Амплитуда и фаза остаточных уровней вибрации (перевод из декартовых координат в полярные)
    qDebug() << "Ожидаемая вибрация:";
    QVector<qreal> residual_ampl3(number_points); // Массив амплитуд
    QVector<qreal> residual_phi3(number_points); // Массив фаз
    m = 0;
    for(int i = 0; i<number_points; i++){
        residual_ampl3[i] = sqrt(F3[m]*F3[m] + F3[m+1]*F3[m+1]);
        if(F3[m] >= 0){
            residual_phi3[i] = qAtan(F3[m+1]/F3[m])*180/M_PI;
        } else {
            residual_phi3[i] = qAtan(F3[m+1]/F3[m])*180/M_PI + 180;
        }
        // Вывод остаточных вибраций
        qDebug() << "Точка "<< i+1 << ":";
        qDebug() << "Амплитуда/Фаза "<< residual_ampl3[i] << "/" << residual_phi3[i];
        m = m + 2;
    }
    return a.exec();
}

Протестировал по DOS-овской программе Гольдина для 2 точки х 1 плоскость и 4 точки х 3 плоскости - результаты схожи.

  • 0
  • 0
  • 0

Полный черновой (можно сократить добавлением переиспользуемых функций) исходный код по пунктам 1-5:

Исходный код 
#include <QCoreApplication>
#include <QTextStream>
#include <QDebug>
#include <QtMath>
#include <QVector>
QTextStream cout(stdout);
QTextStream cin(stdin);
// Функция транспонирования массива
QVector<QVector<qreal>> transposeMatrix(QVector<QVector<qreal>> A, int n, int k){
    QVector<qreal> line(k, 0);
    QVector<QVector<qreal>> B(n,line);
    for(int j = 0; j < k; j++){
        for(int i = 0; i < n; i++){
            B[i][j] = A[j][i];
        }
    }
    return B;
}
// Функция умножения двухмерных матриц
QVector<QVector<qreal>> multiplicationMatrix(QVector<QVector<qreal>> A, QVector<QVector<qreal>> B, int n, int m, int l){
    QVector<qreal> line(m, 0);
    QVector<QVector<qreal>> C(n,line);
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < m; j++)
        {
            for (int k = 0; k < l; k++)
                C[i][j] += A[i][k] * B[k][j];
        }
    }
    return C;
}
// Функция умножения двухмерной матрицы на одномерную
QVector<qreal> multiplicationMatrix2(QVector<QVector<qreal>> A, QVector<qreal> B, int n, int m){
    QVector<qreal> C(n);
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < m; j++)
        {
            C[i] += A[i][j] * B[j];
        }
    }
    return C;
}
// Функция вычисления обратной матрицы
void calculateInverse(QVector<QVector<qreal>>& A) {
    int n = A.size();
    for (int i=0; i<n; i++) {
        // Ищем максимум в этом столбце
        double maxEl = abs(A[i][i]);
        int maxRow = i;
        for (int k=i+1; k<n; k++) {
            if (abs(A[k][i]) > maxEl) {
                maxEl = A[k][i];
                maxRow = k;
            }
        }
        // Меняем местами максимальную строку с текущей строкой (столбец за столбцом)
        for (int k=i; k<2*n;k++) {
            double tmp = A[maxRow][k];
            A[maxRow][k] = A[i][k];
            A[i][k] = tmp;
        }
        // Обнуляем последующие строки в текущем столбце
        for (int k=i+1; k<n; k++) {
            double c = -A[k][i]/A[i][i];
            for (int j=i; j<2*n; j++) {
                if (i==j) {
                    A[k][j] = 0;
                } else {
                    A[k][j] += c * A[i][j];
                }
            }
        }
    }
    // Решаем уравнение Ax = b для верхней треугольной матрицы A
    for (int i=n-1; i>=0; i--) {
        for (int k=n; k<2*n;k++) {
            A[i][k] /= A[i][i];
        }
        // В этом нет необходимости, но результат выглядит лучше:
        A[i][i] = 1;
        for (int rowModify=i-1;rowModify>=0; rowModify--) {
            for (int columModify=n;columModify<2*n;columModify++) {
                A[rowModify][columModify] -= A[i][columModify]
                        * A[rowModify][i];
            }
            // В этом нет необходимости, но результат выглядит лучше:
            A[rowModify][i] = 0;
        }
    }
}
// Функция внесения минуса в матрицу
QVector<QVector<qreal>> minusToMatrix(QVector<QVector<qreal>> A, int n){
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
            A[i][j] = -A[i][j];
    }
    return A;
}

int main(int argc, char *argv[])
{
    setlocale(LC_ALL,"Russian");
    QCoreApplication a(argc, argv);
    int number_points; // Количество точек измерений
    int number_planes; // Количество балансировочных плоскостей
    qDebug() << "Введите количество точек измерений:";
    cin >> number_points;
    qDebug() << "Введите количество балансировочных плоскостей:";
    cin >> number_planes;
    qDebug() << "Введите амплитуду/фазу нулевого пуска (исходная вибрация):";
    QVector<qreal> sensitivity(2*number_points); //обобщенные чувствительности (понадобится в дальнейшем)
    // Заполняем массивы амплитуды и фазы данными 0 пуска
    QVector<qreal> ampl(number_points); // Массив амплитуд 0 пуска
    QVector<qreal> phase(number_points); // Массив фаз 0 пуска
    for(int i = 0; i < number_points; i++){
        cin >> ampl[i];
        cin >> phase[i];
    }
    qDebug() << "Амплитуды" << ampl;
    qDebug() << "Фазы" << phase;
    QVector<qreal> ampl_projections(2*number_points); // Массив проекций на оси X и Y
    int k = 0;
    for(int i = 0; i < number_points; i++){
        ampl_projections[k] = ampl[i]*qCos(qDegreesToRadians(phase[i]));
        ampl_projections[k+1] = ampl[i]*qSin(qDegreesToRadians(phase[i]));
        k = k + 2;
    }
    qDebug() << "Проекции: " << ampl_projections;
    // Данные пробных балансировочных пусков
    QVector<qreal> weight(number_planes); // Массив масс грузов
    QVector<qreal> alpha(number_planes); // Массив углов установки грузов
    QVector<qreal> line1(number_planes, 0);
    QVector<QVector<qreal>> ampl2(number_points, line1); // Массив амплитуд пусков с пробными грузами
    QVector<QVector<qreal>> phase2(number_points, line1); // Массив фаз пусков с пробными грузами
    for(int j = 0; j < number_planes; j++){
        qDebug() << "Пуск №" << j+1 << ":";
        qDebug() << "Введите массу пробного груза, установленного в плоскости №" << j+1 << ":";
        cin >> weight[j];
        qDebug() << "Введите угол установки пробного груза, установленного в плоскости №" << j+1 << ":";
        cin >> alpha[j];
        qDebug() << "Введите амплитуду/фазу пробного пуска №" << j+1 << ":";
        for(int i = 0; i < number_points; i++){
            cin >> ampl2[i][j];
            cin >> phase2[i][j];
        }
    }
    qDebug() << "Амплитуды" << ampl2;
    qDebug() << "Фазы" << phase2;
    // Матрица чувствительностей при нормировании к единичным массам
    QVector<qreal> line2(2*number_planes, 0);
    QVector<QVector<qreal>> a_projections2(2*number_points,line2); // Массив проекций векторов влияния на оси X и Y (в соответствии с алгоритмом)
    int row;
    int col=0;
    for(int j = 0; j < number_planes; j++){
        row = 0;
        for(int i = 0; i < number_points; i++){
            a_projections2[row][col] = round(((ampl2[i][j]*qCos(qDegreesToRadians(phase2[i][j])) - ampl_projections[row])*weight[j]*
                                              qCos(qDegreesToRadians(alpha[j])) + (ampl2[i][j]*qSin(qDegreesToRadians(phase2[i][j])) - ampl_projections[row+1])*weight[j]*
                                             qSin(qDegreesToRadians(alpha[j])))/(weight[j]*weight[j])*1000000)/1000000;
            a_projections2[row+1][col] = round(((ampl2[i][j]*qSin(qDegreesToRadians(phase2[i][j])) - ampl_projections[row+1])*weight[j]*
                                               qCos(qDegreesToRadians(alpha[j])) - (ampl2[i][j]*qCos(qDegreesToRadians(phase2[i][j])) - ampl_projections[row])*weight[j]*
                                               qSin(qDegreesToRadians(alpha[j])))/(weight[j]*weight[j])*1000000)/1000000;
            a_projections2[row][col+1] = a_projections2[row+1][col]*(-1);
            a_projections2[row+1][col+1] = a_projections2[row][col];
            row = row + 2;
        }
        col = col + 2;
    }
    qDebug() << "Матрица чувствительностей: " << a_projections2;
    QVector<qreal> line3(2*number_points, 0);
    QVector<QVector<qreal>> a_projections2_t(2*number_planes,line3); // Транспонированный массив a_projections2[][]
    a_projections2_t = transposeMatrix(a_projections2, 2*number_planes, 2*number_points);
    qDebug() << "Транспонированная матрица чувствительностей: " << a_projections2_t;
    QVector<QVector<qreal>> A(2*number_planes,line2);
    A = multiplicationMatrix(a_projections2_t, a_projections2, 2*number_planes, 2*number_planes, 2*number_points);
    qDebug() << "Матрица А: " << A;
    // Расчет обратной матрицы
    // Входные данные
    QVector<qreal> line4(4*number_planes,0);
    QVector<QVector<qreal>> A2(2*number_planes,line4);
    // Передаем в вектор А2 массив a_projections2_x[][]
    for (int i=0; i<2*number_planes; i++) {
        for (int j=0; j<2*number_planes; j++) {
            A2[i][j] = A[i][j];
        }
    }
    // Дополняем матрицу диагональю единичек (требует метод расчета обратной матрицы)
    for (int i=0; i<2*number_planes; i++) {
        A2[i][2*number_planes+i] = 1;
    }
    calculateInverse(A2);
    qDebug() << "Обратная матрица А2: " << A2;
    // Удаляем добавочные столбцы
    QVector<QVector<qreal>> B(2*number_planes,line2); // Массив обратной матрицы
    for (int i = 0; i < 2*number_planes; i++)
    {
        for (int j = 0; j < 2*number_planes; j++)
            B[i][j]=A2[i][j+2*number_planes];
    }
    // В соответствии с алгоритмом вносим минус в обратную матрицу
    QVector<QVector<qreal>> C(2*number_planes,line2); // Mатрица -B[][]
    C = minusToMatrix(B, 2*number_planes);
    // Умножаем все это дело на транспонированную матрицу проекций
    QVector<QVector<qreal>> D(2*number_planes,line3); // Промежуточная матрица умножения
    D = multiplicationMatrix(C, a_projections2_t, 2*number_planes, 2*number_points, 2*number_planes);
    qDebug() << "Матрица D: " << D;
    // И умножаем на исходную матрицу вибраций - получаем матрицу весов
    QVector<qreal> weights_matrix(2*number_planes); // Матрица весов
    weights_matrix = multiplicationMatrix2(D, ampl_projections, 2*number_planes, 2*number_points);
    qDebug() << "Матрица weights_matrix: " << weights_matrix;
    // Вычисление величин и положений уравновешивающих масс
    qDebug() << "Расчетное положение балансировочных грузов:";
    QVector<qreal> cargo_weight(number_planes); // Массив масс расчетных балансировочных грузов
    QVector<qreal> cargo_phi(number_planes); // Массив углов установки балансировочных грузов
    int l = 0;
    for(int i = 0; i<number_planes; i++){
        cargo_weight[i] = sqrt(weights_matrix[l]*weights_matrix[l] + weights_matrix[l+1]*weights_matrix[l+1]);
        if(weights_matrix[l] >= 0){
            cargo_phi[i] = qAtan(weights_matrix[l+1]/weights_matrix[l])*180/M_PI;
        } else {
            cargo_phi[i] = (qAtan(weights_matrix[l+1]/weights_matrix[l])*180/M_PI + 180);
        }
        qDebug() << "Плоскость №"<< i+1 << ":";
        qDebug() << "Масса = "<< cargo_weight[i] << ", " << "Угол = "<< cargo_phi[i];
        l = l + 2;
    }
    // Далее необходимо вычислить остаточную вибрацию после установки расчетных грузов
    // Умножаем матрицу проекций на матрицу весов
    QVector<qreal> E(2*number_points); // Промежуточный массив
    for (int i = 0; i < 2*number_points; i++)
    {
        for (int j = 0; j < 2*number_planes; j++){
            E[i] += a_projections2[i][j]*weights_matrix[j];
        }
    }
    // Матрица остаточных уровней вибрации
    QVector<qreal> F(2*number_points); // Массив проекций остаточных вибраций
    for(int i=0; i<2*number_points; i++){
        F[i] = E[i] + ampl_projections[i];
    }
    // Амплитуда и фаза остаточных уровней вибрации (перевод из декартовых координат в полярные)
    qDebug() << "Остаточные вибрации:";
    QVector<qreal> residual_ampl(number_points); // Массив амплитуд
    QVector<qreal> residual_phi(number_points); // Массив фаз
    int m = 0;
    for(int i = 0; i<number_points; i++){
        residual_ampl[i] = sqrt(F[m]*F[m] + F[m+1]*F[m+1]);
        if(F[m] >= 0){
            residual_phi[i] = qAtan(F[m+1]/F[m])*180/M_PI;
        } else {
            residual_phi[i] = qAtan(F[m+1]/F[m])*180/M_PI + 180;
        }
        // Вывод остаточных вибраций
        qDebug() << "Точка "<< i+1 << ":";
        qDebug() << "Амплитуда/Фаза "<< residual_ampl[i] << "/" << residual_phi[i];
        m = m + 2;
    }
    //////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
    int equation;
    qDebug() << "Нужно ли выравнивание остаточных вибраций? (0 - да, 1 - нет):";
    cin >> equation;
    if(equation == 0){
        // Далее выполним выравнивание остаточных вибраций (минимизируем максимальные)
        qDebug() << "Выравнивание остаточных вибраций:";
        qreal rms; // СКЗ остаточных вибраций по всем точкам контроля
        qreal g_sum = 0; // Сумма остаточных вибраций по всем точкам контроля
        for(int i = 0; i < number_points; i++){
            g_sum += residual_ampl[i];
        }
        qDebug() << "g_sum:" << g_sum;
        rms = sqrt(g_sum/number_points);
        qDebug() << "rms:" << rms;
        QVector<qreal> G(number_points); // Массив взвешивающих коэффициентов для всех точек контроля
        for(int i = 0; i < number_points; i++){
            G[i] = residual_ampl[i]/rms;
        }
        qDebug() << "G:" << G;
        // Умножаем последовательно пары столбцов a_projections2_t[2*number_planes][2*number_points] на G[i]
        QVector<QVector<qreal>> H(2*number_planes,line3); // Транспонированная матрица чувствительностей со взвешивающими коэффициентами
        for(int i = 0; i < 2*number_planes; i++){
            k = 0;
            for(int j = 0; j < number_points; j++){
                H[i][k] = a_projections2_t[i][k]*G[j];
                H[i][k+1] = a_projections2_t[i][k+1]*G[j];
                k = k + 2;
            }
        }
        qDebug() << "H:" << H;
        // Вычисляем матрицу скорректированных значений уравновешивающих масс
        // Умножаем транспонированную матрицу чувствительностей со взвешивающими коэффициентами на матрицу проекций
        QVector<QVector<qreal>> I(2*number_planes,line2); // Массив произведения T[][] x a_projections2[][]
        I = multiplicationMatrix(H, a_projections2, 2*number_planes, 2*number_planes, 2*number_points);
        qDebug() << "I:" << I;
        // Расчет обратной матрицы I[][]
        QVector<QVector<qreal>> I2(2*number_planes,line4);
        // Передаем в вектор I массив I2[][]
        for (int i=0; i<2*number_planes; i++) {
            for (int j=0; j<2*number_planes; j++) {
                I2[i][j] = I[i][j];
            }
        }
        qDebug() << "I2:" << I2;
        // Дополняем матрицу диагональю единичек (требует метод расчета обратной матрицы)
        for (int i=0; i<2*number_planes; i++) {
            I2[i][2*number_planes+i] = 1;
        }
        // Передаем исходную матрицу в функцию расчета
        calculateInverse(I2);
        qDebug() << "I2:" << I2;
        QVector<QVector<qreal>> K(2*number_planes,line2); // Массив обратной матрицы
        for (int i = 0; i < 2*number_planes; i++)
        {
            for (int j = 0; j < 2*number_planes; j++)
                K[i][j]=I2[i][j+2*number_planes];
        }
        qDebug() << "K:" << K;
        // В соответствии с алгоритмом вносим минус в обратную матрицу
        QVector<QVector<qreal>> L(2*number_planes,line2); // Mатрица -K[][]
        L = minusToMatrix(K, 2*number_planes);
        qDebug() << "L:" << L;
        // Умножаем все это дело на транспонированную матрицу проекций (в соответствии с алгоритмом)
        QVector<QVector<qreal>> M(2*number_planes,line3); // Промежуточный массив
        M = multiplicationMatrix(L, H, 2*number_planes, 2*number_points, 2*number_planes);
        qDebug() << "M:" << M;
        // И умножаем на исходную матрицу вибраций - получаем матрицу весов
        QVector<qreal> weights_matrix2(2*number_planes); // Матрица весов
        weights_matrix2 = multiplicationMatrix2(M, ampl_projections, 2*number_planes, 2*number_points);
        qDebug() << "Матрица weights_matrix2: " << weights_matrix2;
        // Вычисление величин и положений уравновешивающих масс
        qDebug() << "Новое расчетное положение балансировочных грузов:";
        QVector<qreal> cargo_weight2(number_planes); // Массив масс расчетных балансировочных грузов
        QVector<qreal> cargo_phi2(number_planes); // Массив углов установки балансировочных грузов
        int l = 0;
        for(int i = 0; i<number_planes; i++){
            cargo_weight2[i] = sqrt(weights_matrix2[l]*weights_matrix2[l] + weights_matrix2[l+1]*weights_matrix2[l+1]);
            if(weights_matrix2[l] >= 0){
                cargo_phi2[i] = qAtan(weights_matrix2[l+1]/weights_matrix2[l])*180/M_PI;
            } else {
                cargo_phi2[i] = (qAtan(weights_matrix2[l+1]/weights_matrix2[l])*180/M_PI + 180);
            }
            qDebug() << "Плоскость №"<< i+1 << ":";
            qDebug() << "Масса = "<< cargo_weight2[i] << ", " << "Угол = "<< cargo_phi2[i];
            l = l + 2;
        }
        // Далее необходимо вычислить остаточную вибрацию после установки расчетных грузов
        // Умножаем матрицу проекций на матрицу весов
        QVector<qreal> E2(2*number_points); // Промежуточный массив
        for (int i = 0; i < 2*number_points; i++)
        {
            for (int j = 0; j < 2*number_planes; j++){
                E2[i] += a_projections2[i][j]*weights_matrix2[j];
            }
        }
        // Матрица остаточных уровней вибрации
        QVector<qreal> F2(2*number_points); // Массив проекций остаточных вибраций
        for(int i=0; i<2*number_points; i++){
            F2[i] = E2[i] + ampl_projections[i];
        }
        // Амплитуда и фаза остаточных уровней вибрации (перевод из декартовых координат в полярные)
        qDebug() << "Новые остаточные вибрации:";
        QVector<qreal> residual_ampl2(number_points); // Массив амплитуд
        QVector<qreal> residual_phi2(number_points); // Массив фаз
        m = 0;
        for(int i = 0; i<number_points; i++){
            residual_ampl2[i] = sqrt(F2[m]*F2[m] + F2[m+1]*F2[m+1]);
            if(F2[m] >= 0){
                residual_phi2[i] = qAtan(F2[m+1]/F2[m])*180/M_PI;
            } else {
                residual_phi2[i] = qAtan(F2[m+1]/F2[m])*180/M_PI + 180;
            }
            // Вывод остаточных вибраций
            qDebug() << "Точка "<< i+1 << ":";
            qDebug() << "Амплитуда/Фаза "<< residual_ampl2[i] << "/" << residual_phi2[i];
            m = m + 2;
        }
        // Расчет обобщенных чувствительностей
        for(int i = 0; i < 2*number_points; i++){
            sensitivity[i] = F2[i] - ampl_projections[i];
        }
    }
    if(equation == 1){
        for(int i = 0; i < 2*number_points; i++){
            sensitivity[i] = F[i] - ampl_projections[i];
        }
    }
    QVector<qreal> sensitivity_ampl(number_points);
    QVector<qreal> sensitivity_phi(number_points);
    m = 0;
    for(int i = 0; i<number_points; i++){
        sensitivity_ampl[i] = sqrt(sensitivity[m]*sensitivity[m] + sensitivity[m+1]*sensitivity[m+1]);
        if(sensitivity[m] >= 0){
            sensitivity_phi[i] = qAtan(sensitivity[m+1]/sensitivity[m])*180/M_PI;
        } else {
            sensitivity_phi[i] = qAtan(sensitivity[m+1]/sensitivity[m])*180/M_PI + 180;
        }
        // Вывод остаточных вибраций
        qDebug() << "Точка "<< i+1 << ":";
        qDebug() << "Чувствительность "<< sensitivity_ampl[i] << "/" << sensitivity_phi[i];
        m = m + 2;
    }
    //////////////////////////////////////////////////////////////////////////////////////////////////////
    // Установка масс
    qDebug() << "Установка масс:";
    QVector<qreal> cargo_weight3(number_planes);
    QVector<qreal> cargo_phi3(number_planes);
    for(int i = 0; i < number_planes; i++){
        qDebug() << "В плоскости "<< i+1 << ":";
        qDebug() << "Масса:";
        cin >> cargo_weight3[i];
        qDebug() << "Угол:";
        cin >> cargo_phi3[i];
    }
    // Раскладываем на проекции и записываем в матрицу весов
    QVector<qreal> weights_matrix3(2*number_planes);
    m = 0;
    for(int i = 0; i < number_planes; i++){
        weights_matrix3[m] = cargo_weight3[i]*qCos(qDegreesToRadians(cargo_phi3[i]));
        weights_matrix3[m+1] = cargo_weight3[i]*qSin(qDegreesToRadians(cargo_phi3[i]));
        m = m + 2;
    }
    qDebug() << "weights_matrix3:"<< weights_matrix3;
    // Далее необходимо вычислить остаточную вибрацию после установки реальных грузов
    // Умножаем матрицу проекций на матрицу весов
    QVector<qreal> E3(2*number_points); // Промежуточный массив
    for (int i = 0; i < 2*number_points; i++)
    {
        for (int j = 0; j < 2*number_planes; j++){
            E3[i] += a_projections2[i][j]*weights_matrix3[j];
        }
    }
    // Матрица остаточных уровней вибрации
    QVector<qreal> F3(2*number_points); // Массив проекций остаточных вибраций
    for(int i=0; i<2*number_points; i++){
        F3[i] = E3[i] + ampl_projections[i];
    }
    // Амплитуда и фаза остаточных уровней вибрации (перевод из декартовых координат в полярные)
    qDebug() << "Ожидаемая вибрация:";
    QVector<qreal> residual_ampl3(number_points); // Массив амплитуд
    QVector<qreal> residual_phi3(number_points); // Массив фаз
    m = 0;
    for(int i = 0; i<number_points; i++){
        residual_ampl3[i] = sqrt(F3[m]*F3[m] + F3[m+1]*F3[m+1]);
        if(F3[m] >= 0){
            residual_phi3[i] = qAtan(F3[m+1]/F3[m])*180/M_PI;
        } else {
            residual_phi3[i] = qAtan(F3[m+1]/F3[m])*180/M_PI + 180;
        }
        // Вывод остаточных вибраций
        qDebug() << "Точка "<< i+1 << ":";
        qDebug() << "Амплитуда/Фаза "<< residual_ampl3[i] << "/" << residual_phi3[i];
        m = m + 2;
    }
    qDebug() << "Введите амплитуду/фазу после установки корректирующих масс:";
    // Заполняем массивы амплитуды и фазы данными
    QVector<qreal> ampl3(number_points); // Массив амплитуд 0 пуска
    QVector<qreal> phase3(number_points); // Массив фаз 0 пуска
    for(int i = 0; i < number_points; i++){
        cin >> ampl3[i];
        cin >> phase3[i];
    }
    qDebug() << "Амплитуды" << ampl3;
    qDebug() << "Фазы" << phase3;
    QVector<qreal> ampl_projections3(2*number_points); // Массив проекций на оси X и Y
    k = 0;
    for(int i = 0; i < number_points; i++){
        ampl_projections3[k] = ampl3[i]*qCos(qDegreesToRadians(phase3[i]));
        ampl_projections3[k+1] = ampl3[i]*qSin(qDegreesToRadians(phase3[i]));
        k = k + 2;
    }
    // Вычисление матрицы векторов невязок между реальными и ожидаемыми векторами вибрации
    QVector<qreal> delta(2*number_points); // Матрица векторов невязок
    for(int i = 0; i < number_points; i++){
        delta[i] = F3[i] - ampl_projections3[i];
    }
    // Скорректированная матрица чувствительностей
    QVector<qreal> N(2*number_points); // Промежуточная матрица Σ(k)(X(i,k)*(P(k)*cosΨ(k))^2), Σ(k)(Y(i,k)*(P(k)*sinΨ(k))^2) из алгоритма
    m = 0;
    for(int i = 0; i < number_points; i++){
        l = 0;
        for(int j = 0; j < number_planes; j++){
            N[m] += a_projections2[m][l]*(cargo_weight3[j]*qCos(qDegreesToRadians(cargo_phi3[j])))*(cargo_weight3[j]*qCos(qDegreesToRadians(cargo_phi3[j])));
            N[m+1] += a_projections2[m+1][l]*(cargo_weight3[j]*qSin(qDegreesToRadians(cargo_phi3[j])))*(cargo_weight3[j]*qSin(qDegreesToRadians(cargo_phi3[j])));
            l = l + 2;
        }
        m = m + 2;
    }
    qDebug() << "N:"<< N;
    QVector<QVector<qreal>> a_projections3(2*number_points,line2); // Массив проекций векторов влияния на оси X и Y (в соответствии с алгоритмом)
    row = 0;
    for(int i = 0; i < number_points; i++){
        col = 0;
        for(int j = 0; j < number_planes; j++){
            a_projections3[row][col] = a_projections2[row][col] + (a_projections2[row][col]*cargo_weight3[j]*qCos(qDegreesToRadians(cargo_phi3[j]))/N[row])*delta[row];
            a_projections3[row+1][col] = a_projections2[row+1][col] + (a_projections2[row+1][col]*cargo_weight3[j]*qSin(qDegreesToRadians(cargo_phi3[j]))/N[row+1])*delta[row+1];
            a_projections3[row][col+1] = a_projections3[row+1][col]*(-1);
            a_projections3[row+1][col+1] = a_projections3[row][col];
            col = col + 2;
        }
        row = row + 2;
    }
    qDebug() << "Матрица чувствительностей: " << a_projections3;
    // Расчет матрицы искомых уравновешивающих масс
    QVector<QVector<qreal>> a_projections3_t(2*number_planes,line3); // Транспонированный массив a_projections2[][]
    a_projections3_t = transposeMatrix(a_projections3, 2*number_planes, 2*number_points);
    qDebug() << "Транспонированная матрица чувствительностей: " << a_projections3_t;
    QVector<QVector<qreal>> AA(2*number_planes,line2);
    AA = multiplicationMatrix(a_projections3_t, a_projections3, 2*number_planes, 2*number_planes, 2*number_points);
    qDebug() << "Матрица АA: " << AA;
    // Расчет обратной матрицы
    // Входные данные
    QVector<QVector<qreal>> AA2(2*number_planes,line4);
    // Передаем в вектор А2 массив a_projections2_x[][]
    for (int i=0; i<2*number_planes; i++) {
        for (int j=0; j<2*number_planes; j++) {
            AA2[i][j] = AA[i][j];
        }
    }
    // Дополняем матрицу диагональю единичек (требует метод расчета обратной матрицы)
    for (int i=0; i<2*number_planes; i++) {
        AA2[i][2*number_planes+i] = 1;
    }
    calculateInverse(AA2);
    qDebug() << "Обратная матрица АA2: " << AA2;
    // Удаляем добавочные столбцы
    QVector<QVector<qreal>> BB(2*number_planes,line2); // Массив обратной матрицы
    for (int i = 0; i < 2*number_planes; i++)
    {
        for (int j = 0; j < 2*number_planes; j++)
            BB[i][j]=AA2[i][j+2*number_planes];
    }
    // В соответствии с алгоритмом вносим минус в обратную матрицу
    QVector<QVector<qreal>> CC(2*number_planes,line2); // Mатрица -B[][]
    CC = minusToMatrix(BB, 2*number_planes);
    // Умножаем все это дело на транспонированную матрицу проекций
    QVector<QVector<qreal>> DD(2*number_planes,line3); // Промежуточная матрица умножения
    DD = multiplicationMatrix(CC, a_projections3_t, 2*number_planes, 2*number_points, 2*number_planes);
    qDebug() << "Матрица DD: " << DD;
    // И умножаем на исходную матрицу вибраций - получаем матрицу весов
    QVector<qreal> weights_matrixA(2*number_planes); // Матрица весов
    weights_matrixA = multiplicationMatrix2(DD, ampl_projections, 2*number_planes, 2*number_points);
    qDebug() << "Матрица weights_matrixA: " << weights_matrixA;
    // Вычисление величин и положений уравновешивающих масс
    qDebug() << "Расчетное положение балансировочных грузов:";
    QVector<qreal> cargo_weightA(number_planes); // Массив масс расчетных балансировочных грузов
    QVector<qreal> cargo_phiA(number_planes); // Массив углов установки балансировочных грузов
    l = 0;
    for(int i = 0; i<number_planes; i++){
        cargo_weightA[i] = sqrt(weights_matrixA[l]*weights_matrixA[l] + weights_matrixA[l+1]*weights_matrixA[l+1]);
        if(weights_matrixA[l] >= 0){
            cargo_phiA[i] = qAtan(weights_matrixA[l+1]/weights_matrixA[l])*180/M_PI;
        } else {
            cargo_phiA[i] = (qAtan(weights_matrixA[l+1]/weights_matrixA[l])*180/M_PI + 180);
        }
        qDebug() << "Плоскость №"<< i+1 << ":";
        qDebug() << "Масса = "<< cargo_weightA[i] << ", " << "Угол = "<< cargo_phiA[i];
        l = l + 2;
    }
    // Далее необходимо вычислить остаточную вибрацию после установки расчетных грузов
    // Умножаем матрицу проекций на матрицу весов
    QVector<qreal> EE(2*number_points); // Промежуточный массив
    for (int i = 0; i < 2*number_points; i++)
    {
        for (int j = 0; j < 2*number_planes; j++){
            EE[i] += a_projections3[i][j]*weights_matrixA[j];
        }
    }
    // Матрица остаточных уровней вибрации
    QVector<qreal> FF(2*number_points); // Массив проекций остаточных вибраций
    for(int i=0; i<2*number_points; i++){
        FF[i] = EE[i] + ampl_projections[i];
    }
    // Амплитуда и фаза остаточных уровней вибрации (перевод из декартовых координат в полярные)
    qDebug() << "Остаточные вибрации:";
    QVector<qreal> residual_amplA(number_points); // Массив амплитуд
    QVector<qreal> residual_phiA(number_points); // Массив фаз
    m = 0;
    for(int i = 0; i<number_points; i++){
        residual_amplA[i] = sqrt(FF[m]*FF[m] + FF[m+1]*FF[m+1]);
        if(FF[m] >= 0){
            residual_phiA[i] = qAtan(FF[m+1]/FF[m])*180/M_PI;
        } else {
            residual_phiA[i] = qAtan(FF[m+1]/FF[m])*180/M_PI + 180;
        }
        // Вывод остаточных вибраций
        qDebug() << "Точка "<< i+1 << ":";
        qDebug() << "Амплитуда/Фаза "<< residual_amplA[i] << "/" << residual_phiA[i];
        m = m + 2;
    }
    //////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
    qDebug() << "Нужно ли выравнивание остаточных вибраций? (0 - да, 1 - нет):";
    cin >> equation;
    if(equation == 0){
        // Далее выполним выравнивание остаточных вибраций (минимизируем максимальные)
        qDebug() << "Выравнивание остаточных вибраций:";
        qreal rms; // СКЗ остаточных вибраций по всем точкам контроля
        qreal g_sum = 0; // Сумма остаточных вибраций по всем точкам контроля
        for(int i = 0; i < number_points; i++){
            g_sum += residual_amplA[i];
        }
        qDebug() << "g_sum:" << g_sum;
        rms = sqrt(g_sum/number_points);
        qDebug() << "rms:" << rms;
        QVector<qreal> G(number_points); // Массив взвешивающих коэффициентов для всех точек контроля
        for(int i = 0; i < number_points; i++){
            G[i] = residual_amplA[i]/rms;
        }
        qDebug() << "G:" << G;
        // Умножаем последовательно пары столбцов a_projections2_t[2*number_planes][2*number_points] на G[i]
        QVector<QVector<qreal>> H(2*number_planes,line3); // Транспонированная матрица чувствительностей со взвешивающими коэффициентами
        for(int i = 0; i < 2*number_planes; i++){
            k = 0;
            for(int j = 0; j < number_points; j++){
                H[i][k] = a_projections3_t[i][k]*G[j];
                H[i][k+1] = a_projections3_t[i][k+1]*G[j];
                k = k + 2;
            }
        }
        qDebug() << "H:" << H;
        // Вычисляем матрицу скорректированных значений уравновешивающих масс
        // Умножаем транспонированную матрицу чувствительностей со взвешивающими коэффициентами на матрицу проекций
        QVector<QVector<qreal>> I(2*number_planes,line2); // Массив произведения T[][] x a_projections2[][]
        I = multiplicationMatrix(H, a_projections3, 2*number_planes, 2*number_planes, 2*number_points);
        qDebug() << "I:" << I;
        // Расчет обратной матрицы I[][]
        QVector<QVector<qreal>> I2(2*number_planes,line4);
        // Передаем в вектор I массив I2[][]
        for (int i=0; i<2*number_planes; i++) {
            for (int j=0; j<2*number_planes; j++) {
                I2[i][j] = I[i][j];
            }
        }
        qDebug() << "I2:" << I2;
        // Дополняем матрицу диагональю единичек (требует метод расчета обратной матрицы)
        for (int i=0; i<2*number_planes; i++) {
            I2[i][2*number_planes+i] = 1;
        }
        // Передаем исходную матрицу в функцию расчета
        calculateInverse(I2);
        qDebug() << "I2:" << I2;
        QVector<QVector<qreal>> K(2*number_planes,line2); // Массив обратной матрицы
        for (int i = 0; i < 2*number_planes; i++)
        {
            for (int j = 0; j < 2*number_planes; j++)
                K[i][j]=I2[i][j+2*number_planes];
        }
        qDebug() << "K:" << K;
        // В соответствии с алгоритмом вносим минус в обратную матрицу
        QVector<QVector<qreal>> L(2*number_planes,line2); // Mатрица -K[][]
        L = minusToMatrix(K, 2*number_planes);
        qDebug() << "L:" << L;
        // Умножаем все это дело на транспонированную матрицу проекций (в соответствии с алгоритмом)
        QVector<QVector<qreal>> M(2*number_planes,line3); // Промежуточный массив
        M = multiplicationMatrix(L, H, 2*number_planes, 2*number_points, 2*number_planes);
        qDebug() << "M:" << M;
        // И умножаем на исходную матрицу вибраций - получаем матрицу весов
        QVector<qreal> weights_matrix2(2*number_planes); // Матрица весов
        weights_matrix2 = multiplicationMatrix2(M, ampl_projections, 2*number_planes, 2*number_points);
        qDebug() << "Матрица weights_matrix2: " << weights_matrix2;
        // Вычисление величин и положений уравновешивающих масс
        qDebug() << "Новое расчетное положение балансировочных грузов:";
        QVector<qreal> cargo_weight2(number_planes); // Массив масс расчетных балансировочных грузов
        QVector<qreal> cargo_phi2(number_planes); // Массив углов установки балансировочных грузов
        int l = 0;
        for(int i = 0; i<number_planes; i++){
            cargo_weight2[i] = sqrt(weights_matrix2[l]*weights_matrix2[l] + weights_matrix2[l+1]*weights_matrix2[l+1]);
            if(weights_matrix2[l] >= 0){
                cargo_phi2[i] = qAtan(weights_matrix2[l+1]/weights_matrix2[l])*180/M_PI;
            } else {
                cargo_phi2[i] = (qAtan(weights_matrix2[l+1]/weights_matrix2[l])*180/M_PI + 180);
            }
            qDebug() << "Плоскость №"<< i+1 << ":";
            qDebug() << "Масса = "<< cargo_weight2[i] << ", " << "Угол = "<< cargo_phi2[i];
            l = l + 2;
        }
        // Далее необходимо вычислить остаточную вибрацию после установки расчетных грузов
        // Умножаем матрицу проекций на матрицу весов
        QVector<qreal> E2(2*number_points); // Промежуточный массив
        for (int i = 0; i < 2*number_points; i++)
        {
            for (int j = 0; j < 2*number_planes; j++){
                E2[i] += a_projections3[i][j]*weights_matrix2[j];
            }
        }
        // Матрица остаточных уровней вибрации
        QVector<qreal> F2(2*number_points); // Массив проекций остаточных вибраций
        for(int i=0; i<2*number_points; i++){
            F2[i] = E2[i] + ampl_projections[i];
        }
        // Амплитуда и фаза остаточных уровней вибрации (перевод из декартовых координат в полярные)
        qDebug() << "Новые остаточные вибрации:";
        QVector<qreal> residual_ampl2(number_points); // Массив амплитуд
        QVector<qreal> residual_phi2(number_points); // Массив фаз
        m = 0;
        for(int i = 0; i<number_points; i++){
            residual_ampl2[i] = sqrt(F2[m]*F2[m] + F2[m+1]*F2[m+1]);
            if(F2[m] >= 0){
                residual_phi2[i] = qAtan(F2[m+1]/F2[m])*180/M_PI;
            } else {
                residual_phi2[i] = qAtan(F2[m+1]/F2[m])*180/M_PI + 180;
            }
            // Вывод остаточных вибраций
            qDebug() << "Точка "<< i+1 << ":";
            qDebug() << "Амплитуда/Фаза "<< residual_ampl2[i] << "/" << residual_phi2[i];
            m = m + 2;
        }
    }
    // Окончательная установка масс
    qDebug() << "Окончательная установка масс:";
    QVector<qreal> cargo_weight4(number_planes);
    QVector<qreal> cargo_phi4(number_planes);
    for(int i = 0; i < number_planes; i++){
        qDebug() << "В плоскости "<< i+1 << ":";
        qDebug() << "Масса:";
        cin >> cargo_weight4[i];
        qDebug() << "Угол:";
        cin >> cargo_phi4[i];
    }
    // Раскладываем на проекции и записываем в матрицу весов
    QVector<qreal> weights_matrix4(2*number_planes);
    m = 0;
    for(int i = 0; i < number_planes; i++){
        weights_matrix4[m] = cargo_weight4[i]*qCos(qDegreesToRadians(cargo_phi4[i]));
        weights_matrix4[m+1] = cargo_weight4[i]*qSin(qDegreesToRadians(cargo_phi4[i]));
        m = m + 2;
    }
    qDebug() << "weights_matrix4:"<< weights_matrix4;
    // Далее необходимо вычислить остаточную вибрацию после установки реальных грузов
    // Умножаем матрицу проекций на матрицу весов
    QVector<qreal> EE3(2*number_points); // Промежуточный массив
    for (int i = 0; i < 2*number_points; i++)
    {
        for (int j = 0; j < 2*number_planes; j++){
            EE3[i] += a_projections3[i][j]*weights_matrix4[j];
        }
    }
    // Матрица остаточных уровней вибрации
    QVector<qreal> FF3(2*number_points); // Массив проекций остаточных вибраций
    for(int i=0; i<2*number_points; i++){
        FF3[i] = EE3[i] + ampl_projections[i];
    }
    // Амплитуда и фаза остаточных уровней вибрации (перевод из декартовых координат в полярные)
    qDebug() << "Ожидаемая вибрация:";
    QVector<qreal> residual_ampl4(number_points); // Массив амплитуд
    QVector<qreal> residual_phi4(number_points); // Массив фаз
    m = 0;
    for(int i = 0; i<number_points; i++){
        residual_ampl4[i] = sqrt(FF3[m]*FF3[m] + FF3[m+1]*FF3[m+1]);
        if(FF3[m] >= 0){
            residual_phi4[i] = qAtan(FF3[m+1]/FF3[m])*180/M_PI;
        } else {
            residual_phi4[i] = qAtan(FF3[m+1]/FF3[m])*180/M_PI + 180;
        }
        // Вывод остаточных вибраций
        qDebug() << "Точка "<< i+1 << ":";
        qDebug() << "Амплитуда/Фаза "<< residual_ampl4[i] << "/" << residual_phi4[i];
        m = m + 2;
    }
    qDebug() << "Введите амплитуду/фазу после установки корректирующих масс для сохранения:";
    // Заполняем массивы амплитуды и фазы данными
    QVector<qreal> ampl4(number_points); // Массив амплитуд 0 пуска
    QVector<qreal> phase4(number_points); // Массив фаз 0 пуска
    for(int i = 0; i < number_points; i++){
        cin >> ampl4[i];
        cin >> phase4[i];
    }
    return a.exec();
}
  • 0
  • 0
  • 0

Консольное приложение можно скачать по ссылке . Буду рад, если кто-то протестирует на своих балансировочных программах. На этом первый этап по отработке основных алгоритмов в консольном приложении можно считать оконченным.

  • 0
  • 0
  • 0

Пример работы программы:
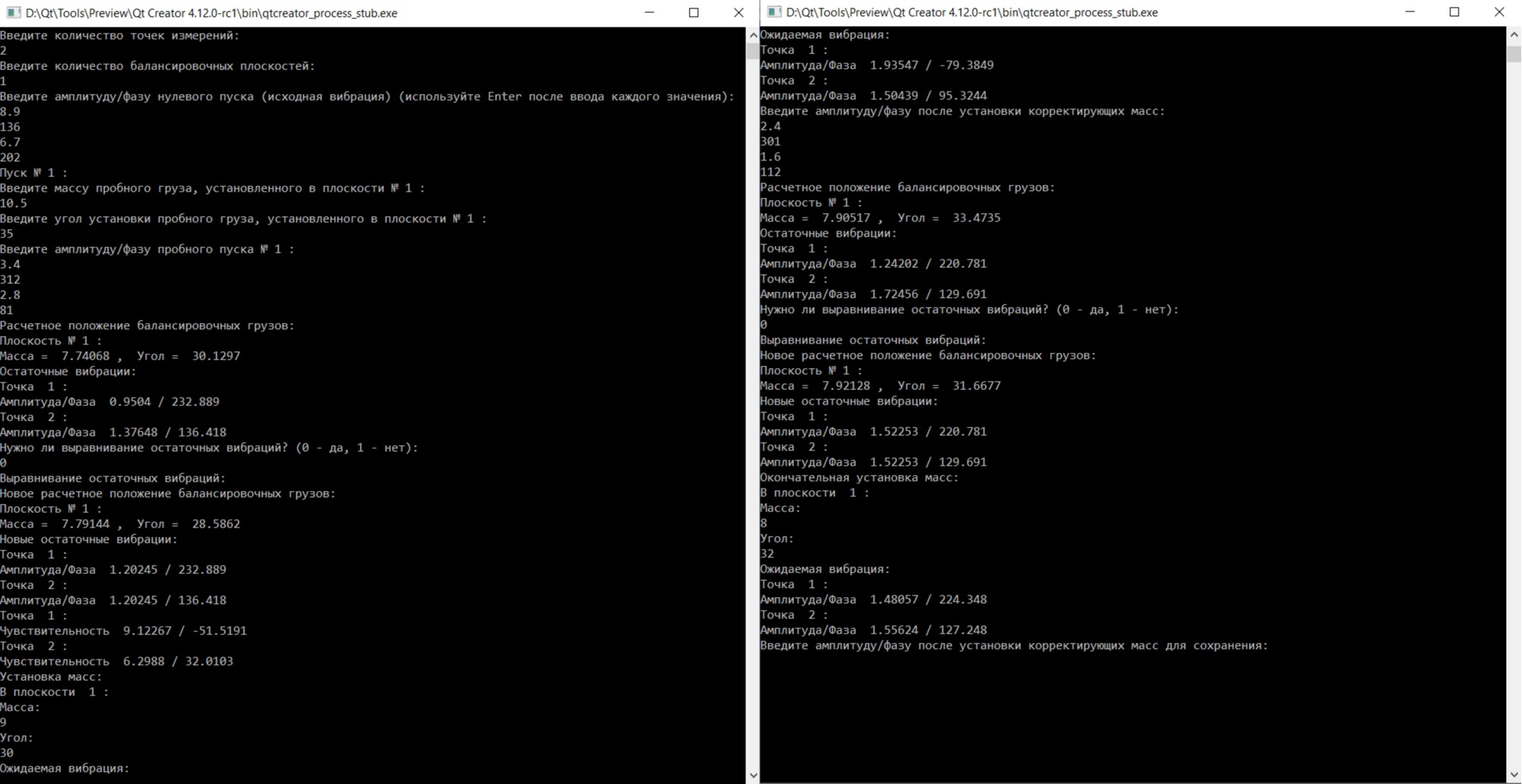
balancing_programm

  • 0
  • 0
  • 0

Этап 2. Разработка ПО на ПК. Достаточно творческая и интересная задача. Хочется сделать интерфейс простым и интуитивно понятным. В качестве основы интерфейс на разбит на 4 блока:
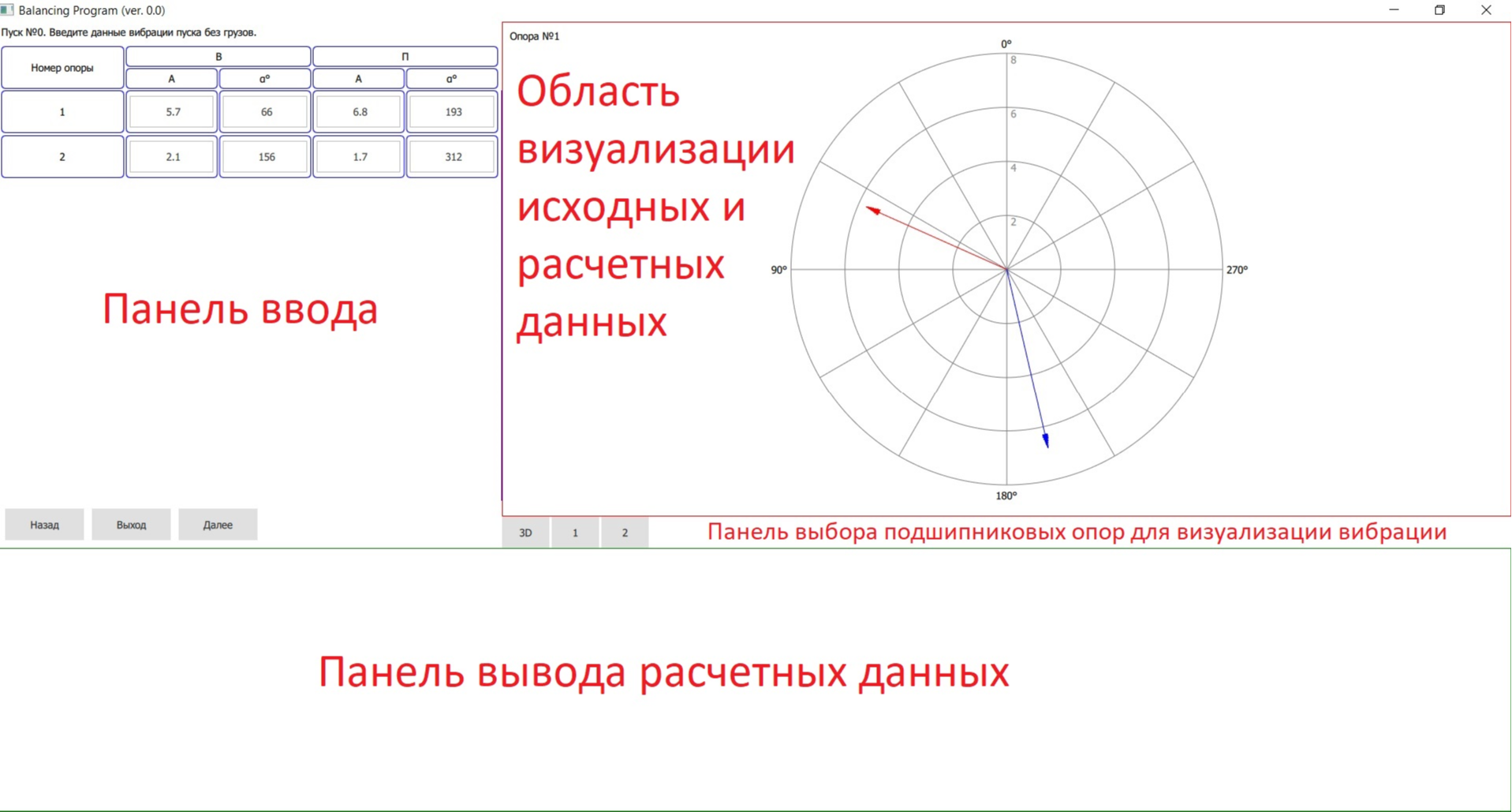
1. Панель ввода данных. В этой панели пользователь вводит данные количества опор, направлений измерений, количества балансировочных плоскостей, исходных и балансировочных пусков, ввод массы и положений пробных и скорректированных грузов, управляет процессом балансировки.
2. Область визуализации исходных и расчетных данных. Исходные и расчетные данные в векторном виде упрощают понимание влияния балансировочных грузов на вибрацию опор. Планируется 2D визуализация вибраций по каждой опоре и 3D визуализация всех вибраций на всех опорах.
3. Панель выбора опор для визуализации. Для выбора желаемого графика.
4. Панель вывода. Сюда будут выводиться расчетные данные.
Это предварительное мое личное видение оптимального интерфейса ПО. Конечно, все может поменяться.
В черновом варианте на данный момент интерфейс выглядит вот так:
Image

  • 0
  • 0
  • 0

Программа обрела некоторый интерфейс и функциональность:

Буду рад любым замечаниям/предложениям.

  • 0
  • 0
  • 0
n
  • July 3, 2020, 10:55 a.m.
  • (edited)

программу можно скачать и протестировать?

  • 0
  • 0
  • 0

Да, в ближайшее время выложу ссылку.

  • 0
  • 0
  • 0

Для тестирования нужно скачать по ссылке BalanceProgram(v.0.0_test)(23,4 МБ) .

Это пока черновой вариант, не добавлен расчет с использованием матрицы невязок (когда реальные результаты балансировки существенно отличаются от расчетных), пока отсутствует регуляризация матрицы (см. методические указания ВТИ, как мне правильно подсказали Вконтакте ), процесс балансировки представляет собой поочередную установку/снятие пробных масс по плоскостям для получения чувствительностей в каждой из них.

Но для простых балансировок боле-менее линейных систем очень даже пойдет уже сейчас. Осталось только потестировать.

  • 0
  • 0
  • 0
n

Спасибо!
у меня есть другая балансировачная программа, для начала с ней сравню результаты, а потом и на практике.

  • 0
  • 0
  • 0

Найдена и устранена ошибка в методике, связанная с отсутствием регуляризации матриц. Доработан интерфейс.
Новая версия доступна по ссылке .

  • 0
  • 1
  • 0

Наконец-то появилось немного времени и накидал программку на Android. Интерфейс и функционал пока такой-же как и для версии на ПК. Теперь можно прикинуть балансировку в полевых условиях. Ссылка для скачивания -> BPmobile.apk .

  • 0
  • 2
  • 0
D

Здравствуйте, программа BPmobile.apk не устанавливается на смартфон.

  • 0
  • 0
  • 0
D

Добрый день. Виталий, вы в какой программе писали BPmobile.apk? Хочу помочь доработать ваш проект? Идея интересная, нехватает только визуализации значений ДКВ что бы внести их в базу данных или элементарно записать на бумагу и метода балансировки по готовым ДКВ.

  • 0
  • 0
  • 0
V
  • June 14, 2022, 12:08 p.m.
  • (edited)

Приветствую всех. Автору огромное спасибо, давно мечтал об многоплоскосном калькуляторе в телефоне.
Тестировал на разных случаях результаты, не сходятся с практичеки получеными решениями. Но когда подставиш готовое решение в "установка нестандартных грузов" результаты расчета вибрация почти 0.
Я правильно понимаю, что здесь не класичекая балансировка по коэффицентам влияния, а чтото среднее между минимизацией устансвливаемых масс и минимизацией вибрации, типа решения задачи оптимизации?

  • 0
  • 0
  • 0

Здравствуйте. Здесь балансировка по коэффициентам влияния, но проблема не в этом. Цель алгоритма - найти решение для системы из n уравнений c m неизвестными, где m>n. В общем случае система не имеет решения. Советский математик Тихонов предложил решать некорректные задачи методом регуляризации, то есть добавить некоторый коэффициент регуляризации, который поможет найти максимально близкое решение. В алгоритме мы тысячи раз решаем нашу систему подставляя разные коэффициенты регуляризации. Получаем некоторую параметрическую L-функцию из набора точек, где каждому коэффициенту регуляризации будет соответствовать решение и невязка (остаточная вибрация). Искомый коэффициент регуляризации будет лежать в точке перегиба этой L-функции, то есть берем ее вторую производную и определяем максимум. Это математическая магия. Но есть один момент - если n = m (система имеет простое решение), то L-функция будет прямой без точки перегиба и необходимо брать краевую точку со сверхмалым коэффициентом регуляризации, чтобы вносимая им ошибка была минимальной. Далее методом наименьших квадратов подравниваем остатки вибрации.

По поводу несходимости результатов. Во-первых алгоритм призван решать задачи из условия линейного отклика системы, но мы живем не в идеальном мире. Во-вторых я выбрал не оптимальный способ подбора коэффициентов для получения L-функции. Грубо говоря я первым подсунул в систему коэф. = 0,000001, а далее каждый последующей увеличивал в 1,2 раза от предыдущего и так 1 млн. раз. Вот если выбрать более оптимальный метод, то можно существенно увеличить точность расчета и время. Но для задач многоплоскостной балансировки промышленного оборудования данное решение видится мне более чем достаточным, не вижу смысла ловить сотые доли виброскорости или десятые доли виброперемещения. С мобильной версией сам балансировал вентиляторы, насосы, электродвигатели - все хорошо. С десктопной версией балансировал турбогенераторы 1200 МВт и по опорам и по ротору - работает чудесно, возможность покрутить вектора через "Установку нерасчетных грузов" помогает найти оптимальный вариант и для ротора и для опор.

"Тестировал на разных случаях результаты, не сходятся с практичеки получеными решениями. Но когда подставиш готовое решение в "установка нестандартных грузов" результаты расчета вибрация почти 0." - я правильно понимаю что несходимость минимальна? Можно данные для воспроизведения проблемы? Если проблема так критична - поправим.

  • 0
  • 0
  • 0
AI

Виталий, спасибо за программу. Пользуюсь ей уже два года. В основном когда в приборе ставлю 2-х плоскостную балансировку, но при первом пробном пуске вижу, что и одной плоскости коррекции достаточно. Тогда рассчитываю груз по Вашей программе, что значительно экономит рабочее время.

  • 0
  • 0
  • 0
I
  • Oct. 4, 2024, 3:47 p.m.

Добрый вечер. Подскажите есть ли обновление .ask? Спасибо.

  • 0
  • 1
  • 0

Здравствуйте. Пока нет. Но в ближайшие дни попробую приступить. Стоит сверхзадача организовать БД балансировок, добавить к расчету по подшипникам балансировку по ротору, добавить учет векторов влияния нагрузки/прогрева, выбор чувствительностей из БД и многое-многое другое. Сами раньше ходили на балансировку со смартфоном, сейчас с планшетом - намного удобнее. Но с балансировкой турбоагрегатов сложнее, очень рутинно подготавливать данные в эксельке, накидывать там вектора нагрузки/прогрева, делать два расчета по подшипникам и ротору раздельно, выискивать данные прошлых балансировок. И аналогичного ПО нет, неоткуда слизать архитектуру и интерфейсные решения. Ну и с математикой в нескольких местах надо будет повозиться в связи с ростом функционала. Вся проблема в основном заставить себя :)
По операционкам приоритет - Windows и Astra Linux, на Android пока не знаю (интерфейс переписывать под небольшие экраны займет время).

  • 0
  • 0
  • 0

Comments

Only authorized users can post comments.
Please, Log in or Sign up
How to become an author?

Learn how to become an author and contribute to the techdiagnost.com community

LEARN

Powered by EVILEG, recommends hosting TimeWeb