Dynamic eccentricity of an induction motor rotor

Finally, let's touch on the topic of the dynamic eccentricity of the electric motor rotor. The defect is relatively rare and interesting. As usual, from my own practice, therefore, further there will be spectra, the search for the cause, and of course photographs.

The subject of the survey is an asynchronous electric motor 4AMU315 manufactured by the Novokakhovsk Electric Machine Building Plant (NKEMZ, Ukraine). Power 160 kW, 3000 rpm. We have more than a dozen such electric motors, and with almost all of them we had problems in terms of vibration and electrical defects.

The body is essentially a steel pipe with ribs and legs welded to it. The huge heavy casing of three millimeter steel does not add to our optimism. Cheap and cheerful. This design does not have sufficient rigidity and on most motors we had to deal with resonances in all directions. One of the electric motors was rewound, and with another one there was a phase loss during the pump running, which led to a strong hum, rapid heating of the case and a decrease in the speed, since they managed to stop and fix the problem in time.

And now, another pump unit recently adopted from the commissioning again “pleased” us with its problems with this electric motor.

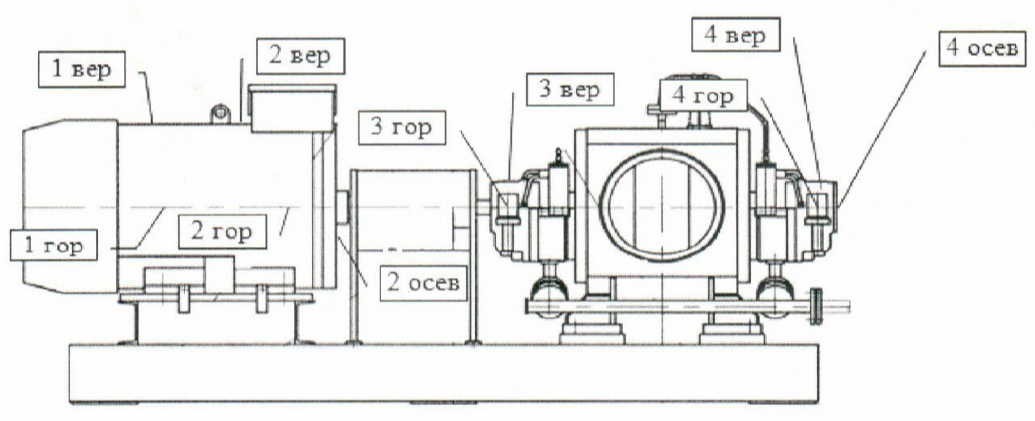
Unit diagram:

Tolerance 4.5 mm / s. Vibration is normal, but the owner of the equipment really does not like the very strong periodic hum from the electric motor (period of about 1.5 seconds), in his opinion, there was a phase failure. In the presence of such a defect, we immediately dissuaded him - our rotation speed did not drop.

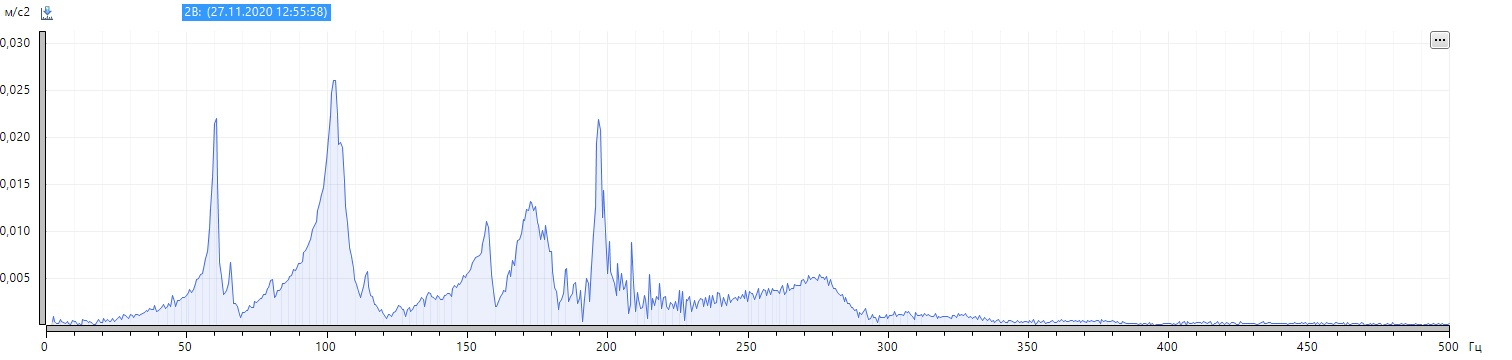
Let's move on to the analysis. As we know, all periodic noises, as well as periodic fluctuations of vibration, are associated with the modulation of closely spaced frequency components. Therefore, we look at the spectrum of vibration velocity.

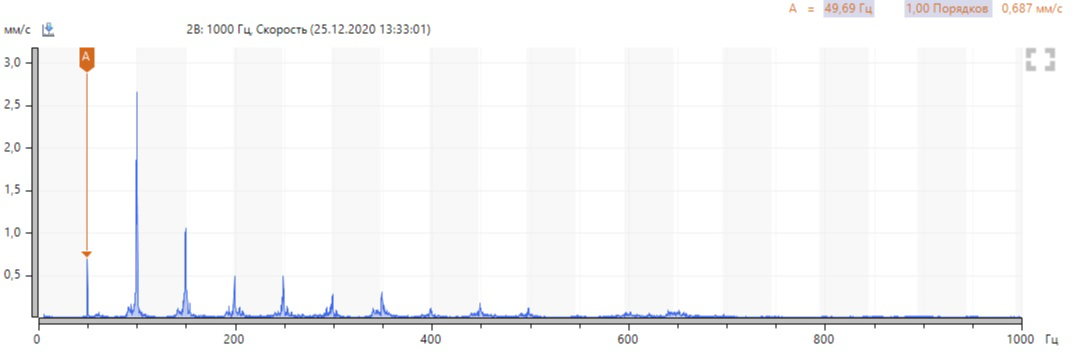
The broad base of each harmonic component of the turnover frequency is striking. Let's increase the spectrum around 100 and 150 Hz:

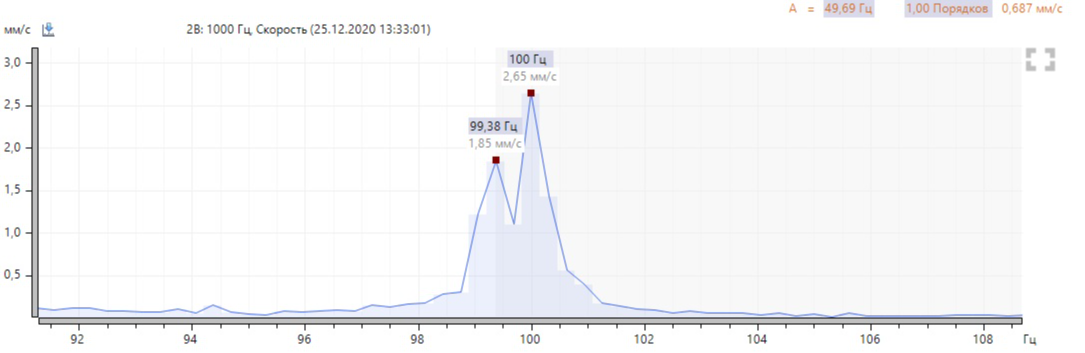
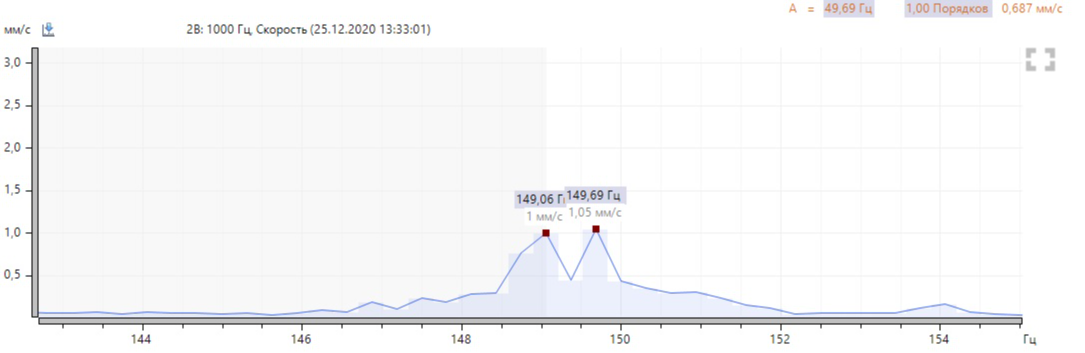
We see two closely spaced frequencies. In fact, there are more side frequency components relative to the turnover harmonics, and we will see them if we increase the frequency resolution in the device settings. The difference between frequencies is 100 - 99.38 = 0.62 Hz. The slip frequency is determined by the difference between the frequency of the electrical network and the rotor speed of 50.00 - 49.69 = 0.31 Hz.

Accordingly, the revolving harmonics are modulated by double slip frequency. The modulation frequency will be approximately 1 / 0.62 = 1.6 seconds. In measurements with a high resolution, we got a period of 1.55 seconds (unfortunately, there is no way to apply those spectra). We see confirmation by a temporary signal:

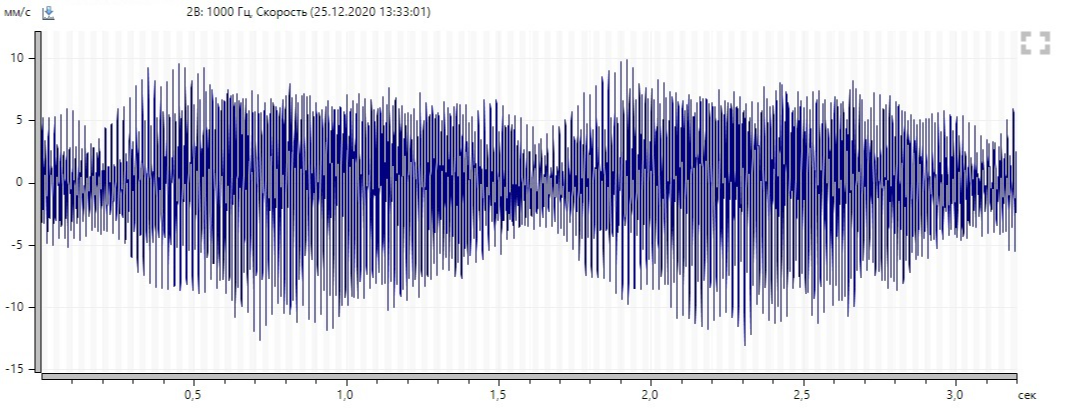
The modulation of these frequencies is the source of periodic hum and vibration fluctuations (in the mode without averaging, the vibration periodically increases and decreases).

Why is the vibration level at point 2B high enough? If we perform a shock test, we will see a natural frequency in the region of 100 Hz, which amplifies the second harmonic of the rotational speed and its lateral components.

It is with such a composition of natural frequencies that I do not like these electric motors.

Now let's go directly to the defect. From the theory we know that the presence of lateral double slip frequencies around the revolving harmonics is characteristic of such defects as rotor rod breakage and rotor dynamic eccentricity. It is very difficult to distinguish these defects, it is practically impossible with sufficient accuracy. Therefore, we send the owner of the equipment a protocol indicating these possible defects and a recommendation to inspect the rotor in our presence (we know our electricians, they have no faith).

During the disassembly of the electric motor, the electricians discovered a weakening of the attachment of the blower impeller to the rotor of the electric motor.

The fasteners were not tightened by the manufacturer, so the impeller was backlash. The electricians were delighted and suggested that this is our problem both in terms of vibration and in terms of strong hum. They demanded to turn the electric motor idling without a casing and a blower impeller.

The vibration did not exceed the permissible values, but the electric motor was noisy, due to the low slip, the hum frequency was already tens of seconds. What we were interested in was that the bearing housing and the rotor were very hot from the side of the blower impeller (about 50 ° C), while they remained cold from the side of the coupling. But the engine did not run for more than 10 minutes at idle speed.

When removing the shield of the electric motor from the free end of the shaft, we made sure that the bearing and lubrication are in perfect condition. They insisted on removing the rotor from the body and inspecting it.
We saw the problem immediately:

The rotor touches the stator around the entire perimeter. The reason was trivial - unsatisfactory manufacturing of the rotor. Visually, it was seen how strongly the aluminum casting of the rods with traces of rubbing protruded from the rotor barrel, while no such protrusions were observed on the opposite side. There is a dynamic eccentricity of the rotor.

Moreover, such eccentricity should create an imbalance, right? Right. And the manufacturer even successfully balanced such a rotor on a machine with balancing weights installed opposite the protruding rods.

The balancing weights themselves were as follows:

Some of the plates dangled freely. Before my eyes is a picture of a balancer with a chisel and a sledgehammer.

Of course, this electric motor can work for more than one hundred hours, but the defect is dangerous because of the magnetic saturation of the tooth zone. The pulsations of the magnetic field in the gap have a deformation effect on the rotor rods and the stator winding. Given that the defective area is located in the area of the stator conductor leads, the risk of insulation wear and short circuit is very likely. In addition, the detected heating of the rotor will negatively affect the bearing life.

If someone has experience in eliminating the dynamic eccentricity of the rotor (groove?), Please share it with us in the comments.